Signalformen und Frequenzspektren von Harmonischen bei Musikinstrumenten
Signalformen und Frequenzspektren von Harmonischen
Bei Musik geht’s neben der Abfolge von Tönen und Klängen genauso um das Zusammenspiel meist mehrerer Instrumente (und in verschiedenen Oktavlagen), die sich passend ergänzen und eben nicht unnötig in die Quere kommen sollen.
Wichtigstes „Messinstrument“ ist dabei immer unser Gehör und natürliches Musikempfinden.
Das Wissen über die Signalformen und die dazugehörigen Frequenzspektren der Harmonischen von Musikinstrumenten ist deshalb nur ein möglicher, ergänzender Blickwinkel. Dieser kann uns aber bei Komposition (Melodien & Harmonien), Sounddesign und Arrangement für ein tieferes Verständnis helfen.
Deshalb ist das Ziel, hier möglichst anschaulich zu zeigen, welche periodischen Signalformen und Anteile von Harmonischen bei verschiedenen Instrumenten (nicht nur Synthesizern!) auftreten. Dabei werden wesentliche Merkmale herausgearbeitet, die im musikalischen (!) Kontext eine wichtige Rolle spielen.
Zu Beginn gibt es einige erklärende Beispiele, wie Schwingungen überhaupt entstehen und dabei Harmonische auftreten. Anschließend werden Signalformen wie eben Sinus, Sägezahn, Rechteck & Co. im Detail besprochen. Weiter wird kurz angerissen, bei welchen Musikinstrumenten diese auftreten.
Dabei bedienen wir uns der Darstellung der Harmonischen und Intervalle auf der Klaviatur in ihrer natürlichen Reihenfolge als visuelles Hilfsmittel, wie wir sie in einem begleitenden Artikel (Link: Intervalle-Harmonische-Frequenzverhältnisse) entwickelt und kennengelernt haben. Dieser klare Bezug zu den Oktaven auf der Klaviatur und vor allem den Intervallen zwischen den Harmonischen soll(te) zum besseren Verständnis beitragen. Schließlich denken wir beim Musikmachen ja nicht in Frequenzen, sondern Noten und Intervallen. In diesem Zusammenhang ist deswegen auch wesentlich wichtiger, wie viele höhere Harmonische ein Instrument erzeugt und wie „dicht“ diese aufeinander folgen, als die exakte mathematische Beschreibung [für letztere gibt’s dicke Formelsammlungen ;-)].
Dass wir nebenbei a bisserl der damit verbundenen Mathematik, Physik und Technik mitnehmen könn(t)en, tut nicht weh und schadet sicher nicht.
Sägezahn als Signalform und in Spektraldarstellung – ein Schnelldurchgang
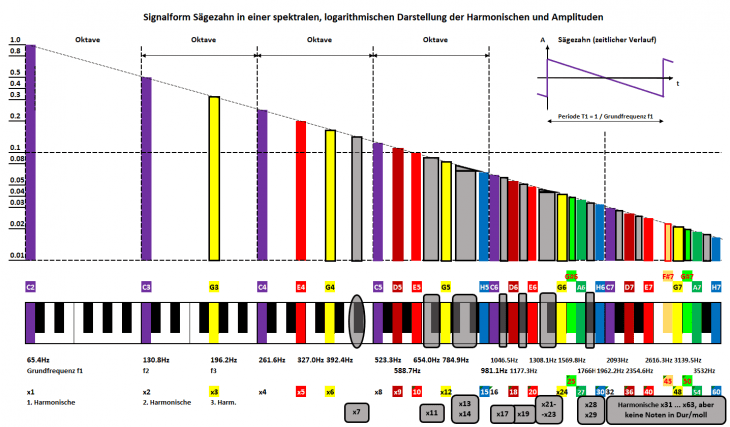
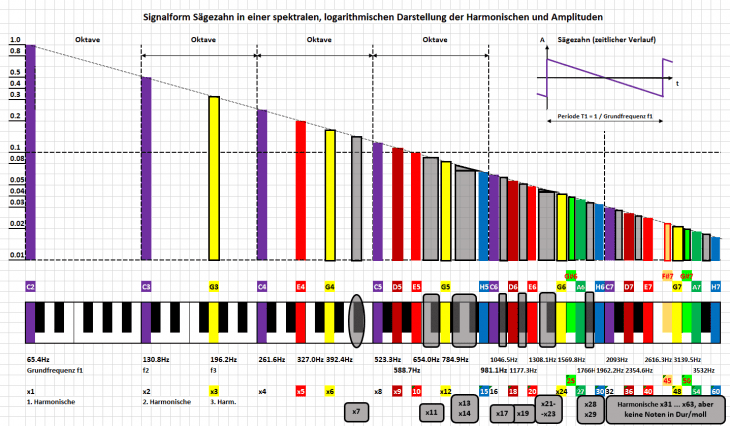
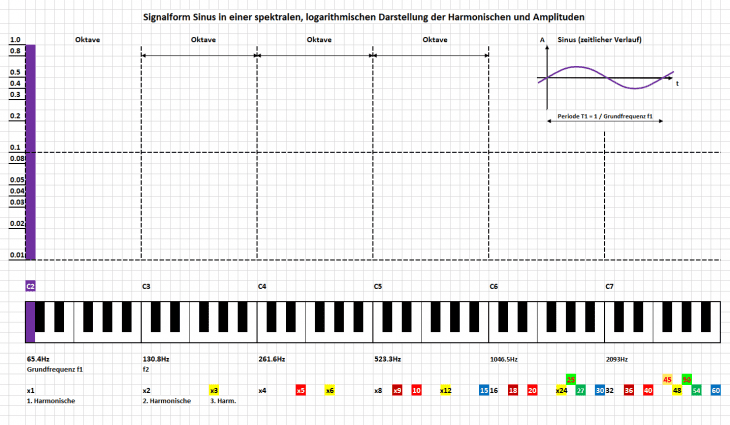
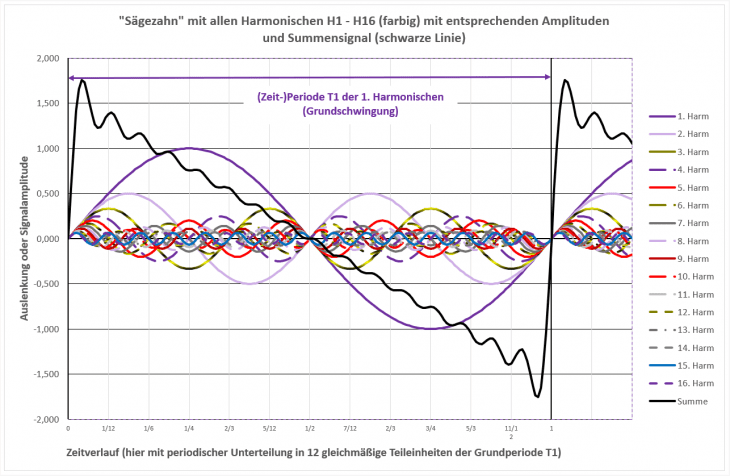
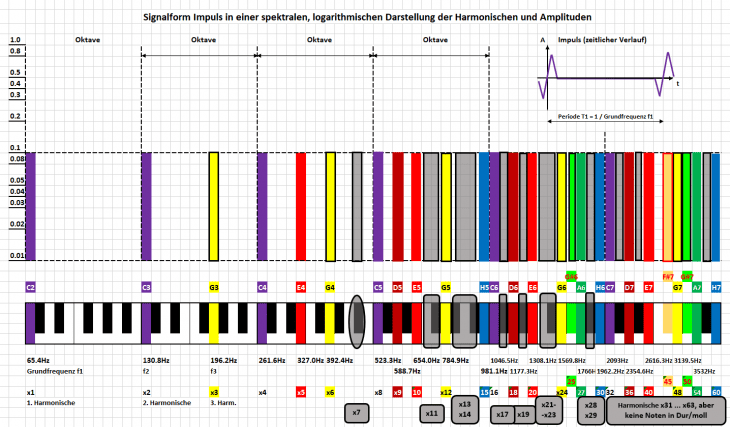
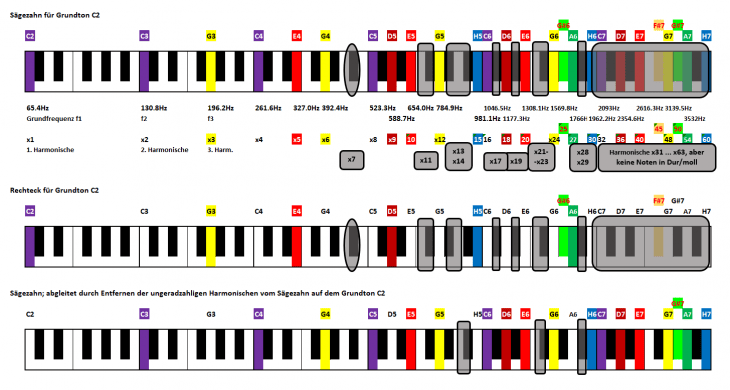
Als Härtetest und Aufhänger fürs Titelbild geht es gleich mal richtig in die Vollen mit einer Signalform, bei der alle Harmonischen vorkommen. Diese hört auf den markanten Namen „Sägezahn“, dessen Ursprung schlicht vom zeitlichen Verlauf des elektrischen Signals (kleines Bild Ecke oben rechts) rührt. Es ist nur ein Durchgang (eine Periode) eingezeichnet, in Realität setzt sich dieses Signal so regelmäßig als Wiederholung weiter fort (angedeutet durch die kurzen Striche).
Weiter in der großen Darstellung dessen Harmonische als ganzzahlige Vielfache der Grundfrequenz, hier gleich wieder basierend auf dem Grundton C2 und der Klaviatur (unten im Bild). So sehen wir unmittelbar, welche der Harmonischen direkt auf Noten zu liegen kommen (diese sind hier mit Farben hinterlegt), und welche „im Graubereich“ zwischen Noten liegen.
Ganz wichtiger Punkt an dieser Stelle: Selbst wenn Harmonische de facto einzelne Sinustöne sind, hören wir diese nicht getrennt, sondern immer nur als Summe. Die Zusammensetzung entscheidet dabei über die „Klangfarbe“, d. h. den Klangcharakter. Das Bild oben ist voll von Harmonischen, somit liegt nahe, dass der Sägezahn somit eine volle, dichte Klangfarbe darstellt – was musikalisch gleich auch gerne dazu genutzt wird, durch passende Überlagerungen mehrerer „Sägezahnsignale“ dichte (Klang-)Teppiche zu legen.
Zentraler Bildbestandteil ist die Spektraldarstellung der einzelnen Harmonischen mit ihren jeweiligen Amplituden („Lautstärken“). Dabei nimmt hier die Höhe der Amplituden der höheren Harmonischen ab. In diesem speziellen Fall sogar exakt mit dem Faktor (1 / N) für die N-te Harmonische. Bei geeigneter – logarithmischer – Pegeldarstellung der y-Achse ergibt sich dann genau die geradlinige Abnahme der Amplituden wie eingezeichnet. Das Bild diesmal bewusst hinterlegt mit dem hübschen Karo-Muster, damit wir in Zeiten von Smartphone und YouTube nicht ganz vergessen, wie unzählige Generationen den guten alten Schreibblock bis zum Ende des letzten Jahrtausends als Hilfsmittel genutzt haben.
Wir bemerken vielleicht eher unbewusst, dass die zeitliche Signalform prinzipiell einen sehr ähnlichen Verlauf aufweist, sich aber regelmäßig fortsetzt (wie angedeutet). Dagegen gibt’s beim Spektrum nur genau einen „Durchgang“. Hier der klare Hinweis, dass diese Ähnlichkeit des Verlaufs nur für diesen ganz speziellen Fall so auftritt. Tatsächlich gilt aber, dass zeitlich periodische – also sich regelmäßig wiederholende – Signale in der Spektraldarstellung nur ganzzahlige Harmonische als einzelne „Spektrallinien“ aufweisen.
Das alles ist sehr viel technische Information, zusammengefasst in einem einzigen Bild.
Bleibt die Frage: Warum ist das so? Aber vielleicht sogar wichtiger: Wozu, was bringt uns das überhaupt?
Für einige ist das sicher schon alles klar und in vielen Details bekannt, verbunden mit der Ungeduld, wie der Autor denn die weiteren Signalformen Rechteck, Puls & Co. illustriert hat. Das findet sich in diesem Betrag weiter unten, versprochen. Wer also will, kann die Abschnitte davor nur kurz überfliegen, ob da auf die Schnelle vielleicht irgendetwas völlig Unbekanntes zu finden ist.
Andere werden sich vielleicht in Anlehnung an Nina Hagen eher denken „… ist ja alles so schön bunt hier …“, was zumindest schon mal jahreszeitlich zur Veröffentlichung dieses Beitrages zu Ostern 2021 passt. Ansonsten viele Fragezeichen à la „Warum alle Harmonischen?“ oder „Warum genau diese Amplitudenabhängigkeiten?“
Das alles wollen wir uns jetzt mal genauer ansehen.
Was braucht’s für die Erzeugung periodischer Schwingungen?
Periodisch heißt regelmäßig wiederkehrend und so was tritt in der Natur nur in Kombination passender „Gegenspieler“, einer geeigneten Anregung und gewissen Randbedingungen auf. „Gegenspieler“ sind hier geeignete Energiespeicher, zwischen denen ein pendelnder, regelmäßiger Energieaustausch stattfindet.
Klingt staubtrocken, daher ein paar anschauliche Beispiele.
Periodische Schwingungen 1 – Schaukel als Beispiel zum Einstieg
Statt jetzt gleich zu versuchen, uns das am Klavier oder Gitarre klarzumachen und zu verstehen, nehmen wir uns erstmal Zeit und gehen auf den (gedanklichen) Spielplatz. Das eine oder andere davon wird uns im Verlauf dann wieder begegnen.
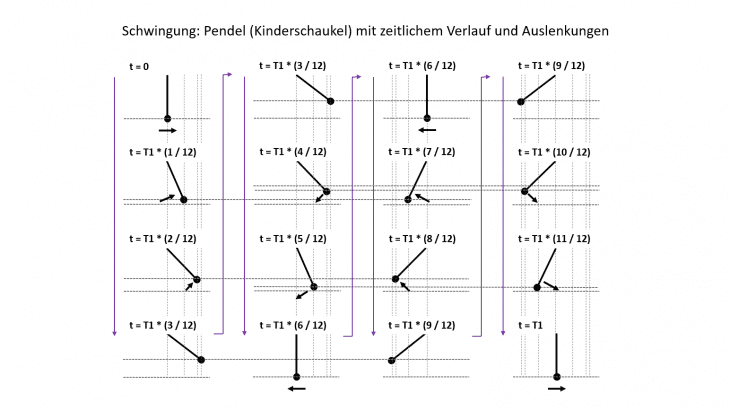
Wir verbinden eine pendelnde Bewegung vielleicht am ehesten mit der beliebten Kinderschaukel. Das passende Video können wir uns sicher sparen, stattdessen gleich eine schematische Darstellung (Schaukel vereinfacht als „Pendel“) mit den zeitlichen Verläufen:
Oh Mann, was’n hier los?!!???
Daher die Beschreibung zu den einzelnen Teilbildchen am Beispiel Schaukelvorgang. 4 x 4 passend zu „outdoor“, wobei diese Anordnung hier eher an die 4 x 4 Matrix bei Grooveboxen oder MIDI-Controller Equipment statt an „offroad“ erinnert. Hauptgrund ist aber lediglich die Darstellung fürs Leseformat.
Wir starten links oben zum Zeitpunkt t = 0. Eine Schaukel ist grad‘ frei, also nichts wie hin, das Kind setzt sich einfach nur drauf und es passiert – gar nichts. Deshalb braucht’s erstmal eine Anregung; in dem Fall also Papi oder Mami, die da erst ein paar Mal anschubsen müssen – daher der Pfeil. So kommt schon mal eine erste Bewegung ins Spiel (es geht dazu in den Bildern weiter nach unten). Die Seile/Ketten der Schaukel wirken dabei als natürliche Randbedingung und geben den Verlauf der Bewegung vor. In diesem Fall also Segmente einer Kreisbahn, da sich die Länge der Seile nicht ändert (und Fliehkräfte nach außen ziehen werden).
„Anschubsen“ bedeutet nur ein kurzer Impuls, aber keine weitere Energiezufuhr. Deshalb wird das Kind nur eine gewisse Höhe erreichen, da Mutter Erde mit ihrer Schwerkraft immer dafür sorgt, dass wir [zumindest körperlich ;-)] nicht die Bodenhaftung verlieren. Im Verlauf dieser Bewegung „nach oben“ wird die Geschwindigkeit deshalb stetig niedriger und geht am höchsten Punkt sogar auf Null zurück (somit kein Pfeil nötig). Das ist im Bild ganz links unten zum Zeitpunkt t = T1 * (3 / 12) gezeigt. Bei diesem ganzen Vorgang haben wir – ohne es groß zu bemerken – „Höhenenergie“ aufgebaut [physikalisch korrekt und zum Angeben: potentielle Lage-Energie im Gravitationsfeld der Erde ;-)]. Es findet also eine vollständige Umwandlung von Bewegungsenergie in Lage-Energie statt. Dieser Zustand ist aber nur von sehr kurzer Dauer, da die Schwerkraft jetzt voll zum Tragen kommt und das Kind auf der Schaukel wieder nach unten zieht. [In der Bildreihenfolge müssen wir jetzt aber erstmal wieder rauf in die zweite Spalte von links; dabei ist der gleiche Zustand t = T1 * (3 / 12) = T1 * (1 / 4) noch einmal wiederholt.]
Dabei kehrt sich die Richtung der Geschwindigkeit um („nach unten“), und wieder sorgen die Seile für eine Bewegung auf einem Kreissegment. Beim Durchgang an der tiefsten Stelle [t = T1 * (6 / 12) = T1 * (1 / 2)] erreicht das Kind dabei die höchste Geschwindigkeit (für die Bewegung in der Waagerechten!) und bewegt sich weiter auf der Bahn, da Papi und Mami vorausschauend schon etwas zurückgetreten sind für den nächsten wichtigen Schritt. Wieder geht’s nach oben (und in die dritte Spalte), und das Spiel beginnt von vorn, allerdings „rückwärts“ in „negativer“ Richtung. Damit das Ganze dann gleichmäßig verläuft oder sogar noch eine größere Höhe erreicht werden kann, schieben die Eltern genau zu dem Zeitpunkt kräftig an, wenn sich das Kind gerade wieder auf dem Weg nach unten macht [t = T1 * (9 / 12) = T1 * (3 / 4)] – da funktioniert’s am einfachsten und besten.
Ergebnis ist eine regelmäßige, pendelnde Bewegung oder eben Schwingung, bei der sinusförmige Bewegungs- und Energieverläufe im Spiel sind.
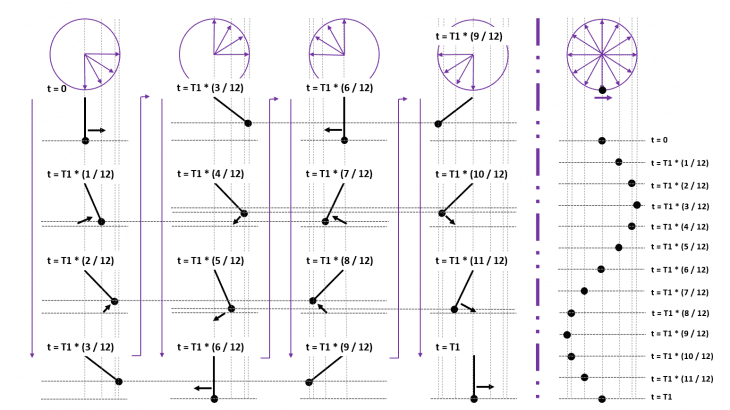
Jetzt kommen die (Hilfs-)Linien ins Spiel, die natürlich wieder nicht so ganz zufällig in all den Bildchen enthalten sind. Denker in großen Kulturen haben sich bereits vor Jahrtausenden intensivst mit dem Kreis beschäftigt. Wir ergänzen die 4 x 4 (Schaukel-)Abfolge deshalb passend mit einer entsprechenden Bewegung auf einer Kreisbahn, hier für die Bewegung in der Waagerechten:
… und auf einmal ergibt die anfangs eher willkürlich wirkende gleichmäßige Aufteilung in 12 zeitliche Teilabschnitte, verbunden mit den ungleichmäßigen Abständen in der horizontalen Bewegung, wesentlich mehr Sinn.
Wenn sich der Pfeil im Kreis oben mit der konstanten (Winkel-) Geschwindigkeit entsprechend der Schaukel bewegt, ergeben sich die gleichen Positionen wie bei der Horizontalbewegung der Schaukel. Das gilt allerdings nur, solange das Verhalten aller Beteiligten (Energiespeicher und „Randbedingungen“) Gesetzmäßigkeiten folgt, die eben genau einen sinusförmigen Verlauf ergeben. Früher gab‘s auf Volksfesten mal Schiffschaukeln, bei denen konnte man übrigens tatsächlich eine komplette Kreisbewegung erreichen – das ganz ohne vorherigen Alkoholgenuss.
Rechts ist dieser gesamte zeitliche Verlauf noch einmal in einem Bild dargestellt; Reihenfolge von oben (t = 0) nach unten zu t = T1, der Dauer genau einer Schwingungsperiode. Die Kurve beginnt zurzeit t = 0 mit einer Amplitude A = 0, erreicht bei t = T1 * (3 / 12) = T1 * (1 / 4) ihren positiven Maximalwert, geht bei t = T1 * (6 / 12) = T1 * (1 / 2) wieder durch Null zur betragsmäßig größten Amplitude in negativer Richtung bei t = T1 * (9 / 12) = T1 * (3 / 4). Am Ende und t =T1 sind wir wieder bei Null angelangt.
Name: Sinus; und das Spiel beginnt wieder von vorne.
In diesem Fall aber auf die Dauer etwas eintönig – eben genau wie auch ein einzelner Sinuston.
Weil das für die Kleinen mit zunehmendem Alter ebenfalls zu langweilig wird, probieren sie dann irgendwann mal aus, welcher Zeitpunkt denn am günstigsten ist, um von der Schaukel abzuspringen und dabei möglichst weit zu fliegen.
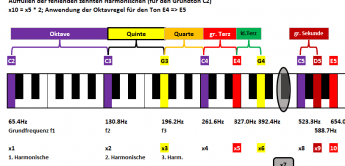
Springen ist das Stichwort zum Wechsel zur entsprechenden Darstellung mit Frequenzen und Harmonischen. Die Frequenz f1 ergibt sich schlicht aus dem Kehrwert der zeitlichen Periode T1, als f1 = (1 / T1). Das hatten wir schon im ersten Artikel, diesmal aber anhand der Schaukel und des Pendels im Detail abgeleitet. Bei einem Sinuston gibt es nur eine Frequenz und somit das einfachste aller Spektren (hier wieder für den Grundton C2):
Da steht er, der einzelne Sinuston (als violetter Balken ganz links beim Grundton C2), einsam und allein wie ein Leuchtturm an der Küste bei Sturm und rauer See. Im Gegensatz zu Letzterem aber mit konstantem „Leuchten“ (hier korrekt natürlich „Tönen“), also konstanter Lautstärke, während die Seeleute draußen auf dem Meer das Leuchtfeuer ja als ein (regelmäßig) wiederkehrendes Lichtsignal sehen. Sofort fällt das Stichwort „Modulation“, womit wir uns aber erst in einer weiteren Folge näher beschäftigen werden.
Jetzt werden alle mit Blick für Details sicher bemerkt haben, dass es bei unserer Schaukelbewegung ja nicht nur eine pendelnde Bewegung in der Waagerechten, sondern auch senkrecht in der Höhe nach oben und wieder nach unten gibt (und hier ja gerade auch der Höhengewinn wichtig für die pendelnden Energien ist). Wieder könnten wir uns die Bewegungsverläufe im Detail ansehen; die entsprechenden Hilfslinien sind ebenfalls eingezeichnet. Tatsächlich lässt sich hier zeigen, dass die Schwingung in der Vertikalen sogar mit der doppelten Frequenz f2 = 2 * f1 stattfindet. Wir können es erahnen, da während eines Durchgangs in der Waagerechten ja zweimal die maximale Höhe und sogar dreimal der tiefste Punkt erreicht wird. Die Schaukel enthält also mehr als eine sehr einfache Bewegung. Wir nehmen weiter bereits mit, dass es unter geeigneten Umständen mehrere Harmonische geben kann. An dieser Stelle sparen wir uns aber die weitere vertiefte Betrachtung, um nicht unnötig mögliche (komplette?) Verwirrung zu stiften.
Somit haben wir zwar schon mal einen besseren Eindruck von pendelnden Energien, Anregung und Randbedingung(en), sowie die Entstehung des sinusförmigen Verlaufs.
Allerdings wirkt bei einigen Musikinstrumenten eine andere Form der Energieumwandlung und -speicherung: „elastische“ Energie oder bildlicher „Federspannung“.
Deshalb und in Anspielung auf mein Pseudonym hier im Forum ein weiteres Gedanken- (!) Experiment, da wir verantwortungsvoll mit Lebensmitteln umgehen (sollten).
Periodische Schwingungen 2 – mit dem Basketball
Dazu braucht’s einen Basketball (passt ja nachdem wir eh schon auf dem modernen Spielplatz sind) und eben einen Krautkopf [für Leser nördlich des Weißwurst-Äquators: Weiß- oder Blaukohl ;-)], um in etwas vergleichbarer Größe zu haben.
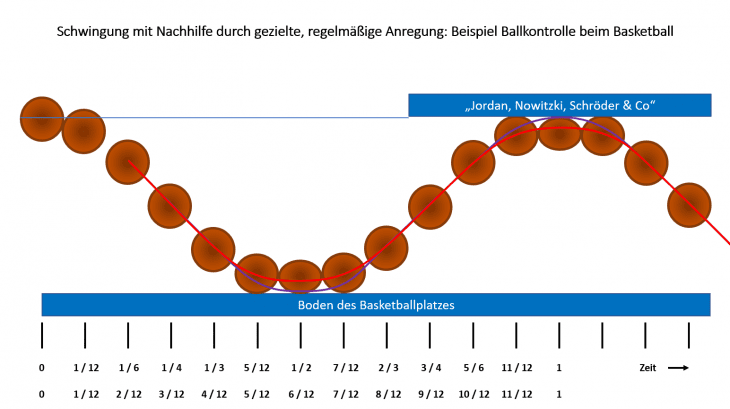
Gleich wieder ein Bild mit einer Darstellung des zeitlichen Verlaufs als Abfolge von Einzelbildern entlang einer Zeitachse, wie wir sie schon von oben her kennen:
Nehmen wir den Basketball in die Hände und lassen ihn auf den Boden fallen, wird er von dort wieder abprallen und zurück in die Höhe fliegen, typisch aber nicht auf die gleiche Höhe wie beim Loslassen (z. B. wegen der Luftreibung). Das Spiel wiederholt sich noch ein paar Mal, wobei die Höhe beim Zurückspringen jedes Mal etwas geringer wird, bis der Ball irgendwann am Boden liegen bleibt. Hat zwar schon was von Schwingung, endet aber und ist damit nicht regelmäßig. Bei einem zweiten Anlauf (wie im Bild gezeigt als zeitlich gestreckte Abfolge der Auf- und Ab-Bewegung) drücken wir den Basketball gleich mal mit Schwung nach unten; und wiederholen das geschickt jedes Mal, wenn der Ball beim Zurückspringen wieder die Höhe unserer Hände erreicht. Schon wird’s etwas Regelmäßiges, das wir zudem auch noch gut kontrollieren können. Mal schneller, mal langsamer, ganz wie’s beliebt. Jordan, Nowitzki, Schröder & Co. machen’s gekonnt vor (deshalb der Block im Bild mit deren Namen als Ersatz für eine Darstellung der Hand). Schneller im Sinne höherer Frequenz lässt sich dabei sowohl durch höhere Kraft als auch die Verringerung der Höhe erreichen („… und immer schön in die Knie gehen …“).
Nun der gleiche Versuch mit dem Krautkopf als Gedankenexperiment (außer wir wollen eh grad‘ Sauerkraut machen). Wir lassen also die Krautkugel fallen und das Ding bleibt – je nach Reifegrad – einfach auf dem Boden liegen. Da haben wir den Salat.
Jetzt zu den Gegenspielern und der Physik. Basketball und Krautkopf fallen dank der Schwerkraft nach unten in Richtung Boden. Ohne zusätzlichen Anfangsschwung (und Luftreibung!) bekommen beide so nebenbei übrigens die gleiche Geschwindigkeit. (Gespeicherte) „Höhenenergie“ verwandelt sich in „Bewegungsenergie“. Nun wissen mir mit ziemlicher Sicherheit, dass sowohl Basketball als auch Krautkopf um Größenordnungen geringeres Gewicht als unsere Erdkugel haben und diese daher beim Aufprall nicht mal nur ansatzweise zu einem Zucken bewegen werden. Wohin diesmal also mit der ganzen „Bewegungsenergie“?
Nun, der Basketball wirkt als elastische Feder, die beim Aufprall zusammengedrückt und damit gespannt wird. (Fast) die ganze „Bewegungsenergie“ geht in gespeicherte Energie als Federspannung über (ein kleiner Teil evtl. in Wärme). Im Bild übertrieben gezeichnet als Verformung in Richtung Rugby-Ei. Sobald alle Bewegungsenergie komplett in Federspannung umgewandelt ist, fehlt die Komponente, die als Gegenspieler zur Federspannung wirkt. Folge: Die Feder entspannt sich und die ganze Energie wird wieder in „Bewegungsenergie“ umgewandelt (Abstoßen vom Erdboden), nur jetzt eben in umgekehrter Richtung. Somit springt der Basketball wieder nach oben. Das aber nur so weit, bis ihn wieder die Realität der Schwerkraft einholt. Deshalb erreicht er nur noch eine gewisse Höhe und kommt dabei zum Stillstand. Also wieder eine Umwandlung, diesmal von „Bewegungsenergie“ zurück zu (gespeicherter) Lage-Energie. Und so geht‘s munter weiter. „Reibung“ führt dabei zu Energieverlusten und verhindert, dass sich das Auf und Ab endlos wiederholen kann. Deshalb braucht’s die Basketballer, die das Spiel hier (weiter)machen ;-). Passendes Stichwort: geeignete, regelmäßige Anregung.
Der zeitliche Bewegungsablauf geht dabei wieder – Überraschung – in Richtung einer Sinusschwingung. Allerdings sind im Bild bewusst zwei Linien enthalten. Lila dabei in Anlehnung an unsere offensichtliche Grundschwingung. Dagegen in rot die Linie, die zusätzlich die Verformung des Balls berücksichtigt, welche die Buckel des Sinus dabei etwas abplattet. Hier sei nur so viel verraten, dass uns das später an geeigneter Stelle wieder begegnen wird.
Unserem nahrhaften Krautkopf fehlt dagegen weitgehend die Elastizität einer Feder. Die ganze „Bewegungsenergie“ bewirkt nur ein Abschütteln von restlicher Erde und einem Auseinanderfallen der Blätter. Zumindest können wir die so aber noch verwerten. Bei einer Melone wär’s dagegen ’ne ziemlich matschige Angelegenheit – selbst schuld, wer hier meinen Hinweis auf „Gedankenexperiment“ ignoriert hat. Wir hätten natürlich genauso einen Kürbis oder Medizinball verwenden können. Wenn das Ding dann aber jemanden auf die Füße fällt, krieg‘ ich mehr Ärger ;-).
Wer sich vielleicht bereits dezent die Frage stellt, ob sich in meinem Krautkopf evtl. ebenfalls etwas zu viel Matsch befinden könnte, der sei an dieser Stelle beruhigt. Der leichte Hauch von Absurdität hat Methode und dient einem guten Zweck.
Wind, Wasser, Wellen
Als vorerst letztes Beispiel die Entstehung von Wellen auf dem Wasser durch Wind.
Die Kraft des Winds kennen wir vom Radfahren bei Gegenwind. Auf Wasseroberflächen bewirkt der Wind durch Reibung ein Anschieben des Wassers. So bildet sich ein mehr oder weniger großer Wasserbuckel („gespeicherte Höhenenergie“). Das zumindest, solange dessen Gewicht und Form nicht so groß wird, dass die Kraft des Winds nicht mehr für ein weiteres Auftürmen ausreicht oder/und die Luftströmung abreißt. Nur ein kleines Zahlenbeispiel, um welche Gewichte wir hier sprechen: Ein Würfel von 1 m x 1 m x 1 m fasst 1.000 Liter Wasser und wiegt mal eben schlappe 1.000 kg. Auf dem Meers Wellen mit solcher Höhe Normalität, da geht wesentlich mehr. Schon beeindruckend, welche Kraft Wind allein durch Reibung erzeugen kann, oder? Wegen dieses Gewichts zieht die Schwerkraft den Wasserbuckel dann auch wieder gnadenlos nach unten, wobei das Wasser wie Basketball und Krautkopf dabei „Geschwindigkeitsenergie“ aufbaut. Nun fließt dieser Überschuss aus dem Wasserbuckel eben genau in solche Bereiche, wo gerade Platz ist – und sich dort wieder Buckel bilden. So entstehen bei entsprechender andauernder Anregung Wasserwellen. Der Begriff „Wellen“ wird dabei für die Ausbreitung und den Energietransport verwendet. Die einzelnen Wassertropfen selbst vollführen dagegen „nur“ eine Schwingung (also z. B. auf und ab oder auch kreisförmig), aber nur in geringem Maße eine Fortbewegung im Sinne langer Strecken.
Endlich: Saiteninstrumente Gitarre und Klavier
Wir ersetzen den Basketball aus unserem (Gedanken-)Experiment und wenden uns den Saiten in unserer Gitarre und Klavier zu, die ebenso gespannt sind wie wir in der Erwartung, was sich denn nun damit so alles anstellen lässt. Bei „gespannt“ liegt „Federspannung“ schon allein begrifflich sehr nahe – da sollten sich doch auch irgendwie Schwingungen erzeugen lassen.
Ab jetzt in Kurzform ;-):
Saiten sind bereits mit einer gewissen Spannung am Instrumentenkörper befestigt. Damit haben wir einerseits schon einen möglichen Energiespeicher, andererseits zudem gleich noch eine Randbedingung: Die Saiten können sich an diesen Enden überhaupt nicht bewegen und das ist in diesem Zusammenhang sehr wichtig für die resultierenden Schwingungs- und Signalformen.
Die Anregung erfolgt bei Harfe, Laute und Akustikgitarre durch „Zupfen“ mit den Fingerkuppen sowie bei der E-Gitarre mit dem Plektrum, bei härteren Spielarten eher in Richtung hämmernder, impulshafter Anschlag. Letzteres ist genau das Prinzip bei Klavier und Flügel, wo über den Tastenanschlag ein Hämmerchen mehr oder weniger stark direkt auf die Saite schlägt. Beides führt zu einer Auslenkung der Saite (und damit Geschwindigkeitszunahme). Dabei bestimmt die Anschlagstärke, wie weit die maximale Auslenkung der resultierenden (Saiten-)Schwingung werden kann, bevor die zugeführte Energie nicht mehr ausreicht, um die Saite (noch) weiter zu spannen. Deshalb stoppt die Bewegung der Saite an diesem Punkt dann kurzzeitig und kehrt gleich darauf ihre Bewegungsrichtung um – es folgt das bekannte Spiel. Mit den schwingenden Bewegungen der Saite wird auch die sie umgebende Luft verdichtet und wieder entspannt – dabei entstehen Schwingungen im Luftdruck, die sich als Schallwellen ausbreiten (mit dem damit verbundenen Energietransport zu anderen Orten im Raum). Genau das hören wir dann bei akustischen Instrumenten als Schall und Ton.
Wie lange die Schwingung bei einmaligem Anschlag andauert, hängt mit von Eigenschaften der verwendeten Materialien ab. Diese, verbunden mit Länge und Spannung der Saite, bestimmen auch den natürlichen Grundton und mögliche Harmonische.
Interessant ist hier, an welchem Ort die Anregung durch Zupfen oder Schlagen erfolgt.
Damit kommen wir endlich zu unseren Harmonischen, denn die spektrale Zusammensetzung und Anteil einzelner Harmonischer hängt mehr oder weniger stark davon ab.
In den seltensten Fällen werden wir die Saiten genau in der Mitte der beiden Einspannpunkte anregen und das hat seine guten Gründe.
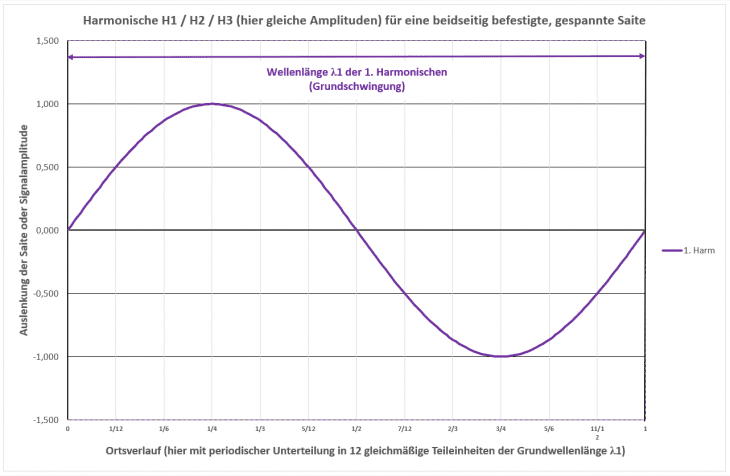
Deshalb hier noch mal das Bild mit einer Sinusschwingung auf dem Grundton, also der 1. Harmonischen. Dabei betrachten wir die Sinus-Linie dieses Mal aber als die gespannte Saite selbst, wie sie während der Schwingung ausgelenkt wird (hier gedanklich den Zahlenwert „1“ links mit der Längeneinheit 1 mm oder bei langen Saiten oder/und harter Spielweise auch 1 cm):
Die Schwingungsform (hier Sinus) tritt somit nicht nur zeitlich, sondern auch als örtliche Auslenkung auf. Ein kompletter Durchgang in der Ortsdarstellung wird als Wellenlänge λ bezeichnet. Frequenz f und Wellenlänge λ sind in der Akustik über die Schallgeschwindigkeit (in Luft!) c miteinander mit einer einfachen Regel verknüpft:
Wellenlänge λ = Schallgeschwindigkeit c / Frequenz f
Einfache Merkregel: bei 27° C beträgt die Schallgeschwindigkeit ca. 330 m/s. Ein Ton mit einer Frequenz von f = 330 Hz [ = 300 * 1/s ] hat in Luft also eine Wellenlänge von genau 1 m. Praktisch u. a. dafür, um aus den Abmessungen eines Raumes die ersten sog. Raummoden (Resonanzen) abzuschätzen. Prinzipiell sollte es auch für die Länge von Saiten so gelten und ist z. B. beim Flügel ja auch anhand der verschiedenen Längen zu erkennen. Allerdings unterstützt die Spannung der Saiten hier zusätzlich.
Zur Erinnerung an die „Randbedingung“: Die Saite ist links wie rechts festgeklemmt und kann sich deshalb dort eben überhaupt nicht bewegen (Geschwindigkeit dort also gleich Null – das brauchen wir später noch mal zum Vergleich mit Flöte und Orgelpfeife)!
Deswegen werden sich kurz nach dem Anschlagen bevorzugt auch nur die Teiltöne oder Harmonischen zeigen, bei denen die Schwingfrequenz diese Randbedingung bestmöglich erfüllt. [Der Vollständigkeit halber sei erwähnt, dass hier auch eine Schwingung mit halber Frequenz als f1 die Schwingbedingung erfüllt. In dem Fall gibt es die fixen Nulldurchgänge nur ganz links und ganz rechts; in der Mitte kann die Saite dann fröhlich schwingen.]
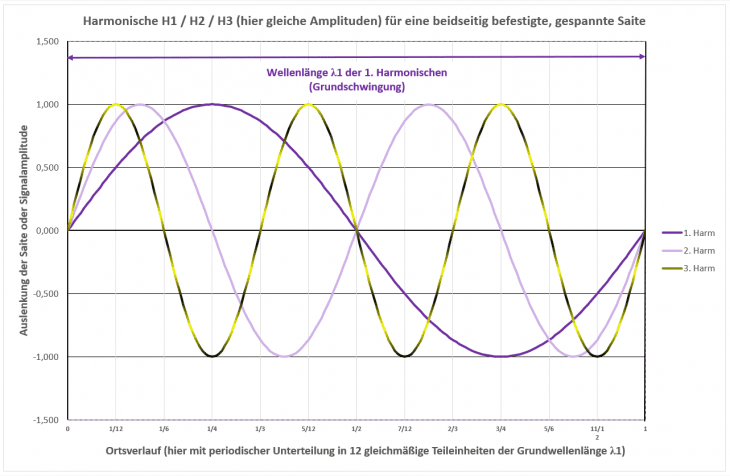
Wir kennen bereits das genau dazu passende Bild mit den Harmonischen 1 / 2 / 3:
An den Rändern ist die Auslenkung „0“, aber wir sehen gleichzeitig, dass sich „erster“ und „letzter“ positiver und negativer Maximalwert der Schwingungsamplitude mit zunehmend höheren Harmonischen immer mehr zu den beiden Rändern bewegt.
Das legt die Vermutung nahe, dass eine Auslenkung genau dort auch (besser) mehrere Harmonische anregen könnte.
Genau so nutzen wir das ja mehr oder weniger ausgeprägt bei Harfe, Gitarre und Klavier: Die Anregung erfolgt eher „einseitig“ in der Nähe eines der beiden Einspannpunkte der Saite. Damit werden eine ganze Menge Harmonischer entsprechend stärker angeregt, was mit zur typischen Klangfarbe des Instruments beiträgt.
Geige und Cello werden dagegen mit einem Bogen „gleichmäßig“ gespielt (oder besser gestrichen), aber selten(er) gezupft oder gar geschlagen. Trotzdem verhält sich die resultierende (Gesamt-)Schwingung am Ende doch recht ähnlich. Bei genauer Betrachtung ist die Anregung eher vergleichbar mit der Reibung von Wind auf dem Wasser: Der Bogen zieht die Saite durch Reibung mit sich, bis die Spannung der Saite irgendwann zu groß wird. Dann befreit sich die Saite fast schlagartig und beginnt so zu schwingen, bis sie wieder vom Bogenstrich mitgenommen wird.
Wie entsteht der „Sägezahn“?
Hier kommt Monsieur Fourier und seine bewiesene Theorie ins Spiel:
Tonale, periodische Klänge lassen sich aus solchen einzelnen Harmonischen bzw. Sinusschwingungen zusammensetzen.
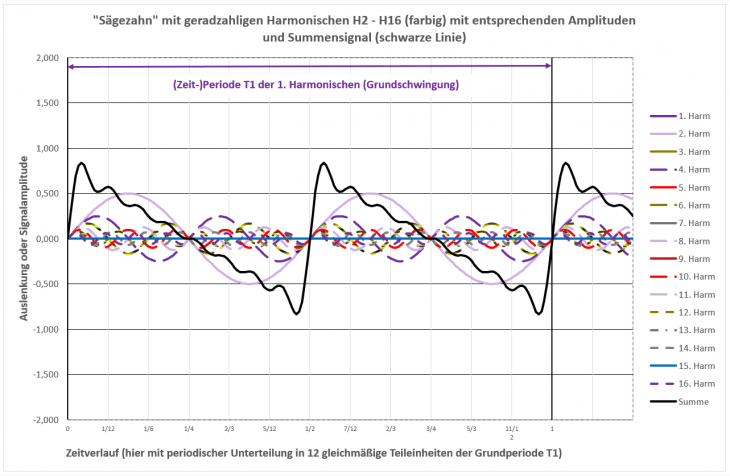
Wir nehmen aus unserem Baukasten mit den herrlich bunten Harmonischen diejenigen mit Nummern 1 bis 16 sowie gleich mit passenden Lautstärken/Amplituden wie eingangs im Titelbild und sehen uns deren zeitlichen Verlauf als Einzelschwingungen wie auch die resultierende, hörbare Gesamtschwingung an – jetzt allerdings wieder als zeitlichen Verlauf, et voilà:
Da ist sie, die Säge!
Dabei muss erwähnt werden, dass es in dieser extrem ausgeprägten in Natur nicht immer auftreten wird, da die Form und Material des Instruments ebenfalls einen Einfluss haben.
Wesentliche Merkmale sind einerseits der (nahezu) geradlinige und gleichmäßige Abfall von der höchsten positiven Amplitude zur betragsmäßig höchsten negativen Amplitude. Die sichtbare, überlagerte (Rest-)Schwingung kommt übrigens davon, weil hier die ganzen Harmonischen ab Nr. 17 aufwärts nicht in der Berechnung berücksichtigt wurden.
Andererseits bemerken wir den extrem kurzen, abrupten Übergang von „maximal negativ auf maximal positiv“, der genau einmal während einer Periode auftritt. „Extrem kurz/abrupt“ heißt schnell,und schnelle zeitliche Vorgänge sind immer mit hohen Frequenzen verknüpft.
Wir erinnern uns und sehen im Bild: Eine Harmonische mit Vielfachen N der Grundfrequenz passt eben genau N-mal in die zeitliche Grundperiode. Heißt aber auch, die Dauer genau einer Periode der N-ten Harmonischen ist eben ein N-tel der Zeit der 1. Harmonischen, also entsprechend kürzer. Schon wieder dieses fröhlich schnatternde & quakende Federvieh ;-).
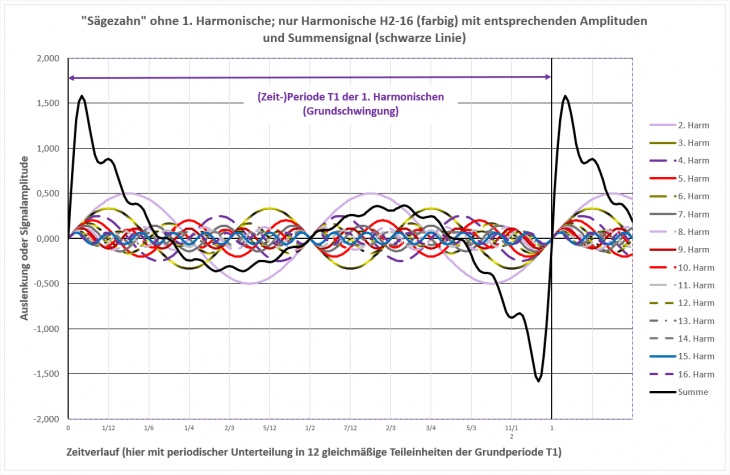
Mit unserem additiven MS Excel Synthesizer lässt sich dieser sehr wichtige Zusammenhang bzgl. schneller, abrupter Übergänge als Resultat einer Vielzahl von (phasen-)richtig überlagerten höheren Harmonischen sehr schön aufzeigen. Dazu entfernen wir im folgenden Bild nur die 1. Harmonische aus der Berechnung und dem Bild; das Ganze sieht dann so aus:
Der gleichmäßige, lineare Abfall ist jetzt komplett verschwunden. Das zeigt klar, dass daran die 1. Harmonische wesentlich beteiligt war/ist.
Geblieben sind dagegen sowohl der positive Puls zu Beginn der Periode als auch der dazugehörige negative Puls am Ende der Periode, verbunden mit dem sichtbaren Anteil der 2. und 3. Harmonischen „im Mittelteil“. Die Gesamtperiode hat dabei aber immer noch die Dauer T1 der 1. Harmonischen! Also werden wir auch dieses Signal auf der gleichen Grundtonhöhe wahrnehmen, allerdings mit einer anderen Klangfarbe.
Allein anhand dieser beiden Bilder sehen wir weiter sehr deutlich, wie sich Schwingungsverläufe durch die richtige Zusammensetzung der einzelnen Harmonischen gestalten lassen.
Impulse & Rauschen
Wir können dieses Spiel noch weitertreiben und die Amplituden aller Harmonischen auf denselben Wert angleichen; d. h. nicht mehr der (1/N) Abfall wie im Titelbild:
Ergebnis ist ein bunter, gleichmäßig hoher Lattenzaun, der vor allem zu höheren Oktaven hin offensichtlich immer dichter wird. Ganz schön eng dort, oder? Im Bereich von C7 – H7 ist der Graubereich in der Spektraldarstellung übrigens ganz bewusst weggelassen, dass wir dort schon mal den schönen Regenbogen sehen können.
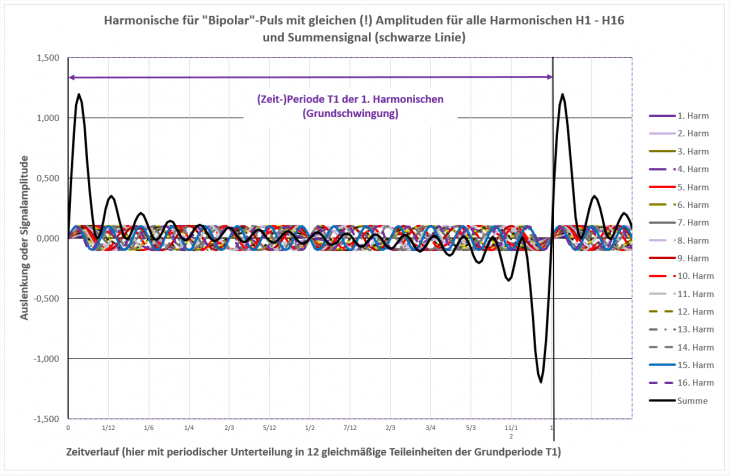
Jetzt das Ganze als zeitlicher Verlauf (allerdings nur für die Harmonischen 1 – 16 mit Amplitude 0.1):
Wie wir sehen, ist das Ergebnis ein noch stärker ausgeprägter Impulsverlauf mit „Geklingel“ im Mittelteil.
Vor allem dürfte so aber der „Nudel“-Salat im „Mittelteil“ auffallen, bei dem die einzelnen Harmonischen optisch nicht mehr klar voneinander zu unterscheiden sind. Das Gleiche gilt für das schwarze Summensignal, welches ebenfalls mehr oder weniger untergeht – wer sagt jetzt „im Rauschen untergeht“?
Bevor wir nun aber in Excel noch mehr Harmonische dazunehmen, mit deren Amplituden spielen und schließlich verzweifeln, bedienen wir uns einer Analogie und wenden uns einer anderen (elektromagnetischen) Schwingungsform zu: dem Licht.
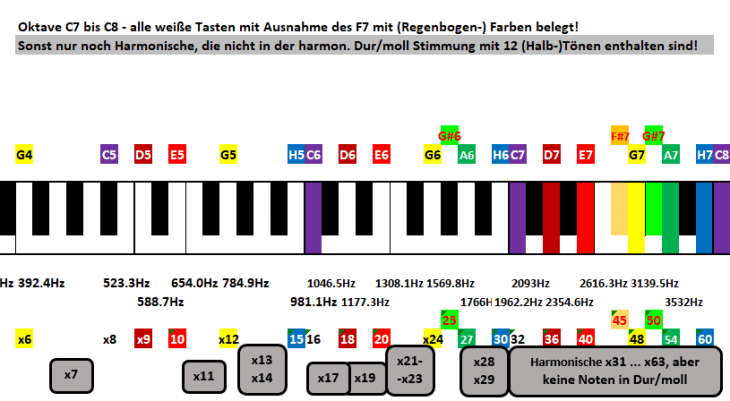
Dazu der passende Detailausschnitt aus unserem Spaziergang durch die Harmonischen, bei dem wir im Bereich C7 bis C8 schon sehr viele Tasten – vor allem fast alle weißen Tasten – mit Farben belegen konnten:
Von C7 bis C8 erstreckt sich ein schöner bunter Regenbogen und natürlich ist genau diese Farbwahl alles andere als Zufall, sondern aus mehreren Gründen sehr gezielt so gewählt.
Rein physikalisch hat Rot die geringeren Frequenzen, Blau dagegen die höheren Frequenzen. Übrigens beträgt der Umfang der Frequenzen des sichtbaren (!) Lichtspektrums nur geringfühgig mehr als exakt 1 Oktave. D. h. blaues Licht hat in etwa die doppelte Frequenz von rotem Licht. Genau das nutzen wir hier, um die Frequenzverdopplung im akustischen Bereich zu veranschaulichen, auch wenn das so im Lichtspektrum eben gerade nicht als periodische Wiederholung auftritt.
Beim Licht werden Rottöne eher als „warm“, Blautöne dagegen eher als „kalt“ wahrgenommen. Im akustischen Frequenzbereich wird von „warmen“ Bässen und „warmen“ Mitten gesprochen, dagegen aber meist eher von „klaren, kalten“ Höhen (Gedanke hier wohl in Richtung „kristallklar“, wie eben Eiskristalle). Das passt so dann aber nur für den Gesamtfrequenzbereich (also nicht jeweils innerhalb einer Oktave).
Interessant dann aber ein weiteres Verhalten von Licht. Farben in genau dieser Anordnung sehen wir in der Natur typisch eben genau nur bei einem Regenbogen oder beim Durchgang von weißem Licht durch ein Prisma. Ganz offensichtlich enthält weißes Licht also alle Farben, aber wir können diese nicht mehr separat wahrnehmen.
„Weißes“ Licht – da liegt doch „weißes“ Rauschen begrifflich schon ganz in der Nähe. Tatsächlich ist weißes Rauschen nichts anderes als ein chaotisches Gemisch von allen Frequenzen (nicht nur von Harmonischen!) und Amplituden. Auf der Klaviatur habe ich ja schon den einen oder anderen „Graubereich“ dazugefügt, bei dem Harmonische eben nicht mehr auf bekannten Tönen einer harmonischen Dur-Moll-Tonleiter liegen. Trotzdem ist selbst bei hohen Frequenzen immer noch Platz zwischen den einzelnen Harmonischen mit Frequenzabstand von jeweils 65,4 Hz bei einem Grundton C2 und Frequenz 65,4 Hz wie hier im Beispiel. Deswegen ergeben die Harmonischen bei höheren Frequenzen kein wirklich weißes Rauschen. Es ist eher so wie beim Blick in den klaren Nachthimmel (in dunklen Gegenden ohne Lichtverschmutzung). wir können im Bereich der Milchstraße zwar viele Sterne sehen, in Wirklichkeit ist zwischen diesen aber noch ein Menge Platz. Für den Sägezahn und seinen höheren Harmonischen gilt das allerdings nur, solange nur ein einzelner Ton gespielt wird.
„Spielereien“ mit Harmonischen
Jetzt ein weiteres Experiment mit unserem Sägezahn: Was passiert denn, wenn wir alle ungeradzahligen Harmonischen inklusive der 1. Harmonischen auf dem Grundton entfernen? Also nur noch die geradzahligen Harmonischen bleiben? Keine Hexerei mit unserem Excel-Synth:
Nanu, wieder ein Sägezahn, nur mit doppelter Frequenz, allerdings eben mit geringerer Gesamtamplitude, da wir die verbleibenden Amplituden nicht angepasst haben.
Das wollen wir doch gleich mal als Spektrum sehen:
Im Bild sind bei der Klaviatur ganz bewusst noch die Nummern der Harmonischen basierend auf dem Grundton C2 enthalten. So wird etwas deutlicher, wo denn die Lücken auftreten. Letztlich verschiebt sich alles um genau ein Oktave nach oben. Wichtiger ist dagegen die Tatsache, dass die verbleibenden Harmonischen wieder eine Sägezahnschwingung bilden, nur bei doppelter Frequenz.
Genau deshalb können wir auch komplexe Klangfarben wie einen Sägezahn so gut im Oktavabstand spielen und mischen – sie ergänzen sich prima und ganz natürlich.
Bis jetzt haben wir Sinus (als einzelne Harmonische auf der Grundfrequenz), Sägezahn, extreme Pulse einerseits sowie „gleichmäßiges“ Rauschen andererseits kennengelernt.
Rechteck und Dreieck – für Orgelpfeife, Klarinette und Flöte
Beim vorherigen Versuch haben wir aus dem vollen Spektrum des Sägezahns alle ungeradzahligen Harmonischen entfernt und nur diejenigen mit geraden Zahlenverhältnissen stehenlassen.
Was passiert also, wenn wir das genau umgekehrt machen, somit nur die ungeraden Harmonischen übrigbleiben?
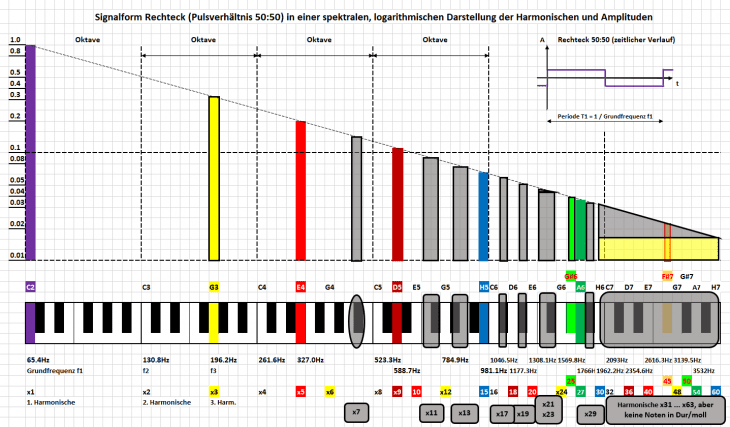
Wir bleiben zunächst in der Spektraldarstellung; und wieder entfernen wir nur Harmonische, aber ändern nichts an den Amplituden:
Rein aus dem Spektrum können wir uns sicher nicht vorstellen, wie der zugehörige Zeitverlauf aussieht. Auffallend dagegen sind sofort die großen Lücken gerade bei den ersten Harmonischen, also zwischen C1 und G3; G3 und E4, usw.
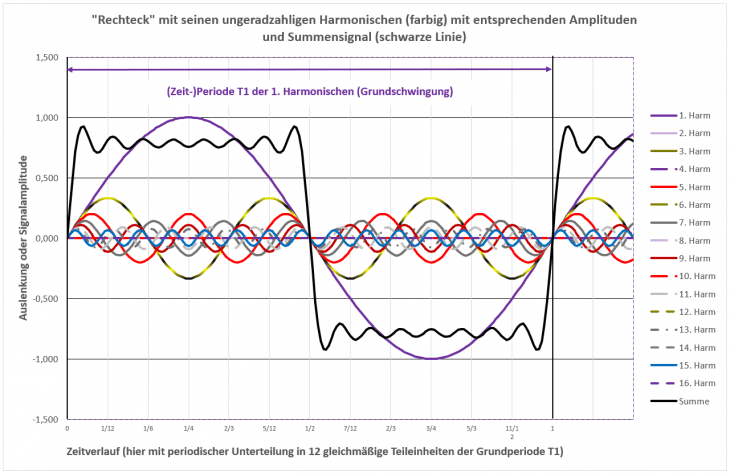
Jetzt das Ganze per Berechnung im Zeitbereich:
Ergebnis ist ein „symmetrisches“ Signal mit rechteckförmigem Verlauf, bei dem der Wechsel von maximaler positiver Amplitude auf die maximale negative Amplitude genau in der Mitte, also T1 * (1 / 2) erfolgt. Entsprechend wird das als Pulsverhältnis ausgedrückt (hier 50 % : 50 %, oder kurz 50 : 50) und am Einstellregler gerne mit Pulsbreite beschrieben.
Das ist also der Synthesizer-Freunden bestens bekannte Rechteck mit seiner im Vergleich zum Sägezahn deutlich unterschiedlichen Klangfarbe. Interessant dabei, dass es gleich zweimal pro Periode diese harten, steilen Übergänge gibt. Das weist bereits wieder auf Spektralanteile gerade bei höheren Frequenzen hin.
Die Überschwinger jeweils an den Flanken sowie das „Geklingel“ in den flachen Bereich kommt auch hier wieder davon, dass wir nur die Harmonischen im Bereich 1 – 16 in die Rechnung einbezogen haben.
Durch geschickte Wahl von Harmonischen konnten wir damit sowohl einen Sägezahn mit der doppelten Frequenz, als auch ein symmetrisches Rechtecksignal mit der gleichen Frequenz erzeugen. Im Umkehrschluss lässt sich daraus ableiten, dass sich aus beiden Letzteren bei richtigen Werten wieder der ursprüngliche Sägezahn zusammenbauen lässt. Bei veränderten Amplituden lassen sich dagegen weitere Klangfarben erzeugen.
Hier noch mal die Harmonischen auf der Klaviatur aus unseren Versuchen im direkten Vergleich:
Durch die fehlenden Harmonischen lässt der Rechteck Platz für die Mischung mit weiteren Signalformen.
Hier als weiteres Beispiel ein Rechtecksignal mit der Grundfrequenz f1 und einem zweiten Rechteck im Oktavabstand, also doppelter Frequenz f2:
Zwar werden nicht alle Harmonischen wie beim Sägezahn aufgefüllt, vor allem fehlen die meisten Oktaven der Grundfrequenz f1. Die Klangfarbe wird insgesamt aber voller und lässt sich durch Mischen beider Signale variieren. Wir stellen aber auch fest, dass es gerade bei den höheren Harmonischen dichter wird, und sich damit noch mehr im Graubereich tummeln wird.
Bei allen bisherigen Betrachtungen haben wir einen wichtigen Parameter und Aspekt außer Acht gelassen, der in der Beschreibung einer Schwingungsform aber ebenfalls von wichtiger Bedeutung ist: die „Phase“.
In der Natur kennen wir die Mondphasen Neumond / Halbmond (zunehmend) / Vollmond / Abnahme / Halbmond (abnehmend); verbunden mit Auswirkungen auf Ebbe und Flut am Meer. Weiter in vielen Kulturen auch aus den Mondperioden abgeleitete Feiertage im Kalender, wie z. B. das Osterfest oder in Asien der Beginn des neuen Mondjahres. In Bereichen deutlich nördlich und südlich des Äquators gibt’s zusätzliche Phasen als ausgeprägte Jahreszeiten.
Bei Schwingungen wird deren Startpunkt als „Phase“ beschrieben, gerade in Bezug auf andere Signale.
Bis jetzt hatte in unseren Betrachtungen mit dem Sägezahn jede einzelne Harmonische ihren Startpunkt exakt bei „0“, und alle Schwingungen liefen der gleichen Richtung los; hier der Detailausschnitt beim Start der Harmonischen:
„Harmonisch“ also im leicht abgewandelten Sinn, dass alle Beteiligten exakt gleichzeitig und dann noch in die richtige Richtung loslaufen.
Das bedarf schon sehr guter Abstimmung, um nicht zu sagen Zwangsmaßnahmen. Beim Chor und Orchester übernehmen Chorleiter und Dirigent diese Aufgabe, verbunden mit dem guten Willen aller anderen Mitstreiter*Innen. Im Stadion erleben wir das in guter Annäherung als kollektiven Aufschrei, wenn einer der Klubs einen Treffer landet [oder es halt doch bloß haarscharf vorbei geht ;-)].
Nun ist aber nicht zu erwarten, dass das genau immer so sein muss – so wie wir das im Bild oben zu jedem anderen Zeitpunkt sehen können.
Im sonstigen täglichen (Zusammen-) Leben wird so ein perfekt synchronisierter Start eher selten so auftreten. Da gibt’s Orte, an denen man das so ja auch gar nicht erwartet, wie z. B. am Bahnhof oder wo eben einfach viele Leute zusammenkommen und wild durcheinanderreden.
An diesem Punkt kommen wir noch mal auf das Rauschen zurück. Neben dem Auftreten aller Frequenzen (also eben nicht ausschließlich von Harmonischen) gibt’s auch eine wild verteilte und sich zeitlich verändernde Mischung von Amplituden und Phasen.
Beispiele dafür in der Natur ist das Rauschen eines Wasserfalls, oder als Ergebnis vieler einzelner Blätter, wenn der Wind durch Laubbäume fegt. Ein sehr schönes Erlebnis hatte ich einmal in der Abenddämmerung beim Überflug eines großen Schwarms von Staren in niedriger Höhe. Es ist schon beeindruckend zu hören, welches Rauschen die kleinen Vögel damit in Summe erzeugen.
Im Folgenden nun ein Beispiel für eine Signalform, bei der neben ausschließlich ungeradzahligen Harmonischen zusätzlich noch eine abwechselnde Folge von gegensätzlichen Phasen und Laufrichtungen der einzelnen Signale auftritt: die Signalform „Dreieck“:
Der Grundton startet wie gewohnt bei „0“ mit Amplitude „0“ wie alle anderen auch (insofern wieder etwas speziell). Die Amplitude der 1. Harmonischen steigt zu positiven Werten an; sie dominiert hier auch klar die resultierende Signalform.
Die 3. Harmonische dagegen läuft sofort in „negative“ Richtung, d.h. zu negativen Amplituden werten. Weiter ist ihre Amplitude diesmal noch geringer. Statt der Abnahme mit dem Faktor 1 / 3 gilt diesmal gleich 1 / 9; gemäß eines Gesetzes (1 / N)².
Nr. 5 folgt dagegen Nr. 1, Amplitude aber nur noch 1 / 25. Nr. 7 schließt sich Nr.3 an mit Amplitude 1 / 49.
Wir sehen, die Phasenlage der einzelnen Harmonischen trägt hier ebenfalls stark zur Form des Summensignals bei.
Der Startpunkt hängt dabei von Randbedingungen ab, es muss übrigens nicht immer zwingend bei „0“ beginnen.
Zuletzt noch die entsprechende Spektraldarstellung:
Das Dreieck ist also eine Signalform mit sehr wenigen Harmonischen, deren einzelne Lautstärken zudem noch sehr stark mit steigender Frequenz abnehmen. Sie kommt dem Sinus daher schon recht nahe und lässt sich wegen der Lücken im Spektrum, vor allem aber wegen des starken Lautstärkeabfalls der höheren Harmonischen, wieder gut mit anderen Signalen mischen/kombinieren.
Gemeinsames Merkmal von symmetrischem Rechteck und Dreieck, wie hier gezeigt, ist das ausschließliche Auftreten von ungeradzahligen Harmonischen. Typische Beispiele von Instrumenten sind Orgelpfeifen, Klarinetten und Flöten. Gerade bei der Kirchenorgel mit ihrer Vielzahl von Pfeifen unterschiedlichster Längen ist der Begriff und Zusammenhang mit der Wellenlänge und Tonhöhe /-frequenz am sichtbarsten. Kurze Pfeifen für hohe Töne und die langen Pfeifen entsprechend für die tiefen Töne. Wer will, gibt sich an dieser Stelle bereits zufrieden.
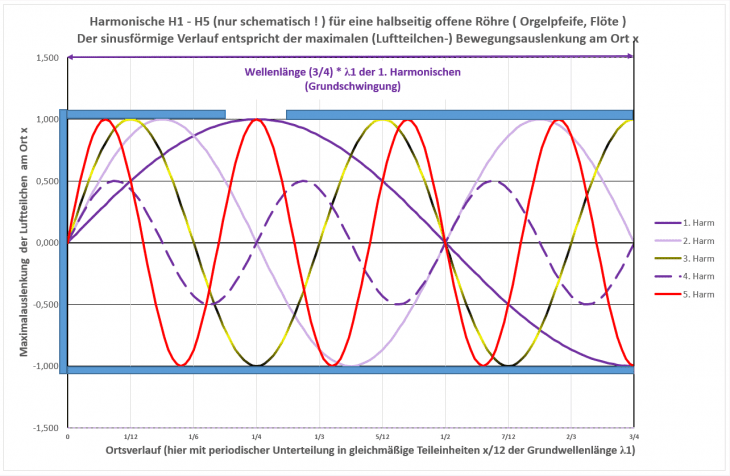
Denn hier ist‘s wirklich nicht mehr so ganz einfach, das mit den bevorzugt ungeradzahligen Harmonischen anschaulich bildlich zu erklären. Das liegt nicht nur daran, dass wir das Verhalten der Luft eben nicht so sehen können, wie man es sich noch bei einer schwingenden Saite vorstellen kann. Tatsächlich geht’s da bereits ans Eingemachte der Ausbreitung von (Schall-) Wellen in (Pfeifen-) Rohren. Daher im nächsten Bild unten nur ein paar Grundgedanken.
Prinzipiell geht’s bei Schallwellen um periodische (Luft-) Druckänderungen und Auslenkung der Luftteilchen.
Bei Saiteninstrumenten konnten wir durch geeignete Randbedingungen – das Festklemmen der Saiten – an genau diesen Befestigungspunkten eine Bewegung der Saite verhindern. Sprich: Dort ist keinerlei Geschwindigkeitsänderung möglich. Für Schallwellen lässt sich das z. B. durch einen harten Abschluss an einem Ende des (Pfeifen-) Rohres erzielen, an dem die Energie der Schallwelle reflektiert wird. Dort ergeben sich maximale Druckänderungen. Das gilt so noch für jede Frequenz und Harmonische. Allerdings soll/muss der Schall ja an einer Stelle aus dem Rohr austreten; schließlich wollen wir was hören. Am effizientesten passiert das für Töne mit Wellenlängen, die an der Austrittsöffnung zu einer maximalen Auslenkung der Schwingbewegung der Luftmoleküle führt. Dann wird auch die Luft außerhalb des Rohres gut anregt. Ist die Länge der Pfeife wie gezeichnet 3/4 der Wellenlänge λ1 des Grundtons, ist genau diese Voraussetzung gegeben, ebenso wie für alle ungeradzahligen Vielfachen. Dagegen weisen geradzahlige Harmonische an der Austrittsöffnung immer einen Nullpunkt bzgl. Auslenkung auf. Im Bild erkennbar als Nullpunkt („Knoten“) rechts für die Harmonischen H2 und H4. Daher treten in Folge bevorzugt nur ungeradzahlige Harmonische auf.
Zusammenfassung und Ausblick
Das war eine ganze Menge Information, die es erstmal zu verdauen gilt. Natürlich können in einem Beitrag dieser Länge nicht alle Themen und Aspekte in allen Details beleuchtet werden.
Vielmehr geht’s darum, Wissen aufzufrischen und eine ergänzende Betrachtungsweise vorzustellen. Wir haben dabei gesehen, welche Harmonischen in welcher Dichte und mit welcher „Reichweite“ zu höheren Oktaven bei verschiedenen Instrumenten bereits beim Spielen nur eines einzigen Tons/tonalen Klangs auftreten. Dieser Blickwinkel mit der Spektral-Darstellung kann somit zum besseren (technischen) Verständnis beitragen, warum sich Instrumente ergänzen, aber auch in die Quere kommen können, wenn sich z. B. ein (ungefilterter) Basslage-Sägezahn in den oberen Oktaven breitmacht. Also für Aspekte der Komposition (Melodien & Harmonien), Sounddesign und Arrangement.
Die hier gewählte optische Verbindung von Harmonischen, Intervallen und der Klaviatur bildet eine direkte Verbindung zum (Tasten-)Instrument.
Die bisherigen Beispiele beschränkten sich auf einen einzelnen Ton oder Töne im Oktavabstand. Deshalb ist natürlich genauso interessant zu sehen und verstehen, wenn Töne in kleineren Intervallen gespielt werden, also bei Melodien oder Akkorden.
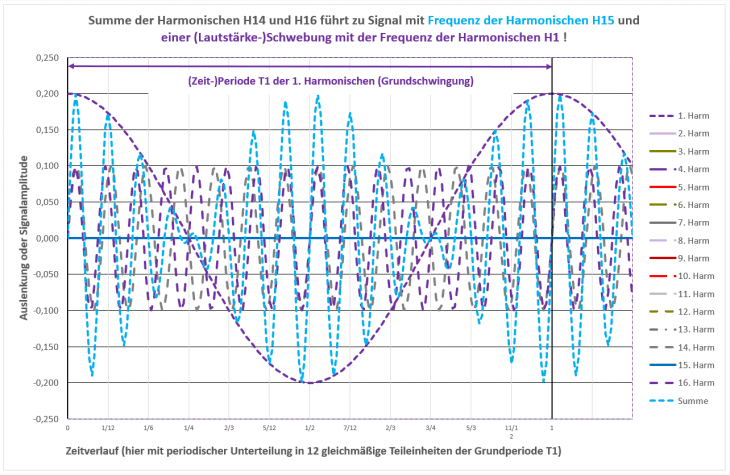
Dazu schwebt mir bereits ein weiterer Artikel vor mit einigen Zahlenspielereien vor, die letztlich zur Anzahl der 12 Töne in der Dur-Moll-Tonleiter führen. Schweben ist dabei ein passendes Stichwort, denn genau das tritt auf, wenn wir uns das Zusammenspiel zwei einzelner, „isolierter“ Harmonischer betrachten (und anhören). Als Vorschau daher dieses Bild mit den beiden Harmonischen H14 und H16, wenn wir nur diese zusammenspielen würden:
Hier ein Link zu einer *.ZIP-Datei, die sämtliche Bilder des Beitrags wie auch die – wieder sehr einfach aufgebaute – Excel-Datei (keine Macros aktiviert) enthält: Signalformen-Spektren-Harmonische
Buchtipps mit den tieferen Details zur Physik mit Beispielen auch für Musikinstrumente und guten Illustrationen:
Physik Lehr- und Übungsbuch, Douglas C. Giancoli, Pearson Studium, ISBN 978-3-86894-023-7
Physik für Wissenschaftler und Ingenieure, Paul A. Tipler Gene Mosca, Spekturm, ISBN 978-3-8274-1945-3
Taschenbusch der Physik, Kuchling, Verlag Harri Deutsch, ISBN 3 8171 1020 0
Übrigens enthält auch das eine oder andere Synthesizer-Benutzerhandbuch Kapitel für Signalformen und Spektren. Aktuelle Beispiele sind Waldorf Quantum und Novation Summit. Zum Virus von Access Music gibt’s ein sehr unterhaltsames Tutorial von Howard Scarr, das die Feinheiten von Instrumenten beleuchtet. Also einfach mal im Support & Download-Bereich der bekannten Hersteller stöbern ;-)













wieder ein erhellender artikel. wie beruhigend, dass mein synthie das alles automatisch macht.
Wenn man das alles verstanden hat und denkt, dass das im richtigen Leben auch immer so ist mit den ganzzahligen Vielfachen, dann darf man nach Inharmonizität googeln.
Und wer schon mal ein Fender Rhodes gestimmt hat mit seinen Metallzungen und sich darüber gewundert hat, dass die Frequenz bei großer Amplitude etwas anders ist als bei kleiner Amplitude, der kann sich damit trösten, dass bei der Herleitung der Theorie nicht alles mit rechten Dingen zugeht. Der Biegewiderstand einer Saite wird vernachlässigt, und man geht z.B. beim Pendel immer von kleinen Auslenkungen aus, sodass man den Sinus des Winkels durch seinen Winkel ersetzen kann.
@bluebell Hach ja, da werden Erinnerungen ans erste Semester „Sprachsignalverarbeitung“ wach. Wenn man dann auch noch alles an seltsamen nichtlinearen Zusammenhängen der Lauschorgane zusammenzählt ist die Verwirrung komplett. Z.B. verändert sich die wahrgenommene Tonhöhe eines Signals mit der Lautstärke, und das auch noch Freuquenzabhängig – verückte Welt!
@t.goldschmitz … was dann gleich die Steilvorlage liefert für einen Beitrag mit Arbeitstitel „Wenn der Mann / die Frau am Pult mal wieder den Mix aufräumen muß … [weil das Arrangement überladen ist ;-)]“.
Also z.B. der durchsetzungsfähige (sprich: ungefilterte) Sägezahn-Bass ordentlich Pegel braucht, damit er auch wirklich Druck im Bassbereich macht, damit aber genauso die oberen Oktaven so richtig schön zukleistert ;-).
@t.goldschmitz es wird noch viel verrückter wenn sich Signale auf dich zu oder von dir weg bewegen – doppler-effekt.
dann darf man sich noch fletcher Munson and masking and Auslöschung durch phase dazu denken,
sogar Lücken im audio werden von unserem Gehirn mit random junk den es sich grad ausgedacht hat gefüllt – ich hab vergessen wie das Phänomen heißt;
und schon bleibt nur noch sehr wenig von unserem ach so eindeutigem Messsignal übrig. ^^
Wunderwelt der Wahrnehmung :)
auf den individuellen Hörapparat (Ohr) sind wir dabei noch gar nicht eingegangen ^^
@bluebell Richtig; „Feinheiten“ wie das Verhalten bei Großsignalanregung und mögliche unharmonische Spektralanteile durch Nichtlinearitäten werden hier in dieser vereinfachten Einstiegsbetrachtung erstmal ganz bewußt ausgeklammert. Allerdings läßt sich gerade das letzte Bild mit den Harmonischen H14 und H16 durch minimale Modifikation ja genauso zur Erklärung von unharmonischen Frequenzanteilen verwenden :-).
Die Bandbreite der Interessen im Leserkreis [und das ist bitte völlig neutral & wertungsfrei zu verstehen ! ] dürfte ja vergleichbar der eines einmalig kurzen Impulses sein. Sprich das Spektrum – um beim Thema zu bleiben – geht vermutlich von „Laß mich mit dieser Mathematik bloß in Frieden“ bis hin zum Naturwissenschaftler, der auch gerne die entsprechende, am besten gleich noch nichtlineare, Schwingungsdifferentialgleichung mit ihren Lösungen sehen möchte ;-).
Daher geht’s erstmal darum, möglichst alle abzuholen und auf die Entdeckungsreise mitzunehmen.
Fast schon eine Doktorarbeit. Danke für den umfassenden und kompetenten Beitrag!!!!
Sehr guter Artikel über die Hintergründe von Frequenzspektren, gratuliere. Beim ersten Bild dachte ich gleich wieder über die Editoren mit solchen Darstellungen. Für mich völlige unsinnig, ganz im Gegenteil zu zweidimensionalen Grafiken. Mit denen kann jeder was anfangen, im Gegensatz zur dreidimensionalen Darstellung.
OK sag schon nix..ausser
Do Re Mi fa Sol la si.
Und nächste Woche befassen wir uns ausgiebig mit dem Penthouse sorry Pentagramm und dessen musikalische Auswirkung auf die seele.grundton eins oberton…danke fùr diesen Bericht.lach.
An alle Leser, die sich über die Basketball-Geschichte wundern: das ist ein schlecht gewähltes Beispiel, da ein hüpfender Ball niemals eine Sinuskurve beschreibt. Richtung Boden hat die Kurve einen spitzen Winkel und nach oben ergibt sich eine Wurfparabel, also eine quadratische Kurve.
Wenn man einen Synthesizer-Bezug sucht, wäre das ein 2-Wege-gleichgerichteter Sinus.
Euer Physiker
@Picard … das schlechte Beispiel eignet sich somit schon mal gut, um auch nichtlineare Schwingungsvorgänge zu erklären ;-).
Scherz beiseite, der Einwand ist aus physikalischer Sicht gerechtfertigt. Mir ist bewußt, daß letztlich all die Beispiele in der Wirklichkeit eben keinen 100% Sinus liefern. Hab‘ das oben auch zum feedback von bluebell kommentiert.
Es geht in erster Linie (und Näherung) darum, sich zuerst mal wieder an einfachen plakativen Beispielen klar zu machen, was es denn überhaupt zur Entstehung von Schwingungen braucht.
Hier mit dem klaren Ziel, die zugehörige Mathematik komplett außen vor zu lassen. Den Fachleuten hier im Forum brauch‘ ich die nicht zu erklären, die haben sie eh drauf.
Versehentlich war die Wahl hier aber tatsächlich nicht; gerade beim Basketball das mit dem übertriebenen „Rugby-Ei“. Geht ja offensichtlich in Richtung „Verzerrung“. Da hab‘ ich auch was vor, wieder ohne Formeln.
Ziel ist letztlich die Spektraldarstellung als (gedankliches) bildhaftes Hilfsmittel anzubieten. Was ist im musikalischen Sinne „harmonisch“, was ist „unharmonisch“, mit möglichst minimaler & einfacher Mathematik und vor allem Bildern.
coole infos.
„probieren sie dann irgendwann mal aus, welcher Zeitpunkt denn am günstigsten ist, um von der Schaukel abzuspringen und dabei möglichst weit zu fliegen.“
hach jaaa…hat mich mal nen armbruch gekostet^^. dafür hatte ich auch ziemlich lange den weitsprungrekord des spielplatzes inner tasche haha
ein blick aufs oscilloscope für irgendwas was ich hören will ist totaler käse.
die verrückt aussehenden Bilder können genauso klingen wie ein puls …
Obacht Selbstbetrug!
wenn ich wissen will was macht meine modulation lohnt sich ein blick aufs oscilloscope.
Also Ohren auf und schön auf die Frequenzanalyse glotzen, da seh ich wenigstens irgendwas was damit zutun hat was ich evtl hören kann. ;)