Programmierworkshop in Python zwecks Manipulation von Obertonspektren (Teil 1)
Hallo AMAZONA! Ich bin MatthiasH und bereits seit Ewigkeiten Leser dieser Plattform. Im Hauptberuf arbeite ich in der Forschung (Informatik/Computergrafik), nachts bin ich eher Musiker. Den Dämmerstunden dazwischen entstammt gewissermaßen die Arbeit, über die ich euch hier berichten möchte.
Inhaltsverzeichnis
Ihr bekommt hier die seltene Gelegenheit, einem Naturwissenschaftler über die Schultern zu schauen, der (außerhalb seiner Kernexpertise wildernd) ein musikalisches Problem entdeckt, daraus eine Forschungshypothese formuliert und diese dann experimentell zu validieren versucht. Ich lade euch ein, mich auf dieser Entdeckungsreise zu begleiten, unterwegs selbst einige Dinge auszuprobieren und mit mir zusammen vor allem viel Spaß dabei zu haben.
Entsprechend der Natur der hier verhandelten Inhalte wird es im Folgenden nicht ganz anspruchslos zugehen. So gibt es unter anderem einen kleinen Programmierworkshop in Audiodatenverarbeitung, und auch ein paar ordentliche Mathebissen erwarten euch. Leser:innen mit einschlägigen Vorkenntnissen und solche, die es einfach mal probieren wollen, sind herzlich eingeladen, ein Python-Notebook aufzuklappen und mitzumachen. Aber auch für alle anderen fällt hoffentlich der eine oder andere interessante Krümel ab. Da es nicht zuletzt auch um Musik geht, muss ich auch hier gewisse Grundkenntnisse in Musiktheorie voraussetzen, werde aber versuchen, euch alle so gut es geht abzuholen. (Vielleicht hilft es hier ja, dass ich selbst kein Experte bin.) Am Ende der Reise steht uns das neuartige Werkzeug der „Overtone F*ckery“ zur Verfügung, mit dem wir Musik für alternative Universen komponieren, neue harmonische Entdeckungen machen oder einfach nur unseren Spaß haben können. Und allerspätestens mit den fertigen Samplesets, auf die ihr leider noch bis zur nächsten Folge warten müsst, steht die Spielwiese dann wirklich jeder Leserin und jedem Leser weit offen.
Das Moll-Dilemma und ein Ansatz zu dessen Lösung
Bei mir begann alles mit dem Konsum eines Videos mit dem großartigen Jacob Collier, den ich hier sicher nicht vorzustellen brauche. Darin beantwortet er „Tech Support“-Anfragen von Musiker:innen und Musikinteressierten aus sozialen Netzwerken und erklärt dabei unter anderem, warum Moll-Akkorde so traurig klingen.
Sie sehen gerade einen Platzhalterinhalt von YouTube. Um auf den eigentlichen Inhalt zuzugreifen, klicken Sie auf die Schaltfläche unten. Bitte beachten Sie, dass dabei Daten an Drittanbieter weitergegeben werden.
Jeder Ton, den ich auf einem x-beliebigen Instrument (von einem Sinusoszillator abgesehen) spiele, bringt neben dem Grundton auch immer eine Reihe von Obertönen mit. Diese bestehen aus ganzzahligen Vielfachen eines Grundtons (die „Harmonischen“), derer es prinzipiell unendlich viele gibt. Im Fall eines „tiefen C“ fängt diese Reihe so an:
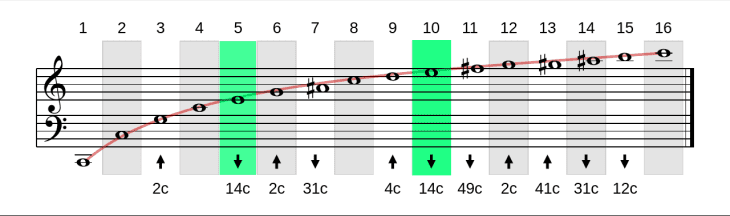
Harmonische Reihe (Obertonreihe). Die Dur-Terzen (5. und 10. Harmonische) sind hervorgehoben.
Angepasst von: https://commons.wikimedia.org/wiki/File:Harmonics.svg (Baba66 unter CC-BY 2.5)
Zweierpotenzen, also die 2., 4., 8., 16., … Harmonischen entsprechen reinen Oktaven. Dazwischen passen aber zu höheren Ordnungen hin immer mehr Zwischentöne. Irgendwann liegen diese so nah beieinander, dass sich nicht mehr sinnvoll in unserem 12-Ton-System aufschreiben lassen. Bei der 3. Harmonischen handelt es sich um die Quinte über der Oktave, ebenso bei der 6., also wiederum der Oktave über ebendieser Quinte. Und die 5. Harmonische liegt eben genau eine große Terz über der 4. Harmonischen. Seit Pythagoras ist eine perfekte große Terz definiert als das Frequenzverhältnis 4:5. Fügen wir die Quinte hinzu, ergibt sich also aus den 4., 5. und 6. Harmonischen ein perfekter Durdreiklang. Drücke ich auf dem Klavier nur eine einzige Taste (am besten hört man es bei den tiefen Tönen), dann spiele ich beispielsweise:
und ohne weiteres Zutun tönet die Obertonreihe in herrlichstem C-Dur (grün markiert):
Wer ein akustisches Klavier zur Verfügung hat, kann durch sanftes Auflegen eines Fingers bei einem Viertel, Fünftel oder Sechstel der Saitenlänge genau diese Teiltöne ausfindig machen und isolieren. Es werden dann alle Frequenzen gedämpft, die an der Position des Fingers keinen Schwingungsknoten haben, und nur die jeweilige Harmonische kann klingen. Die Gitarrist:innen unter euch kennen ja die Flageolettpositionen am 5, 4. und 3. Bund – auch da bekommen wir die 4., 5. und 6. Obertöne und somit einen Durdreiklang – die Physik dahinter ist absolut die gleiche wie beim Klavier. Ohne Fingerauflegen klingen alle Obertöne und formen gemeinsam den charakteristischen Klang des Instruments.
Hier habe ich einmal einen Klavierton mit einem Verfahren, das wir unten noch kennenlernen werden, zu in seine Bestandteile zerlegt. Zunächst erklingt der Originalton, dann beginnend beim Grundton die Obertöne und schließlich wieder die Summe aller Komponenten. Lest beim Hören mal die Notenschrift über diesem Absatz mit und achtet insbesondere auf den (grünen) Durdreiklang, gebildet aus den vierten, fünften und sechsten Teiltönen.
Ein C im Bass schafft also klare Fakten in Richtung C-Dur. Möchte ich darüber aber lieber C-Moll spielen, habe ich erst einmal schlechte Karten. Kennzeichnend für den Mollakkord ist ja eben die kleine Terz, bei C-Moll also das Eb. Das reibt sich aber mit dem E aus der Obertonreihe des Grundtons, das ja nur einen Halbton entfernt ist.
Zusammen klingt es dann dissonant oder traurig oder wie man es auch immer sehen mag.
Hypothese
Für den Hobby-Musikforscher in mir ergab sich daraus nun sozusagen als wissenschaftliche Fragestellung: Klingen Moll-Tonarten besser bzw. konsonanter, wenn das Obertonspektrum des verwendeten Instruments ebenfalls in Moll ist? Intuitiv könnte man ja meinen, dass sich die Teiltöne dann besser vertragen und der Gesamtklang harmonischer wird. Hier eine schematische Darstellung dieser Arbeitshypothese:
Material
Um dieser Frage auf den Grund zu gehen, brauchen wir zunächst Versuchsmaterial. Für ersteres wähle ich ein frei erhältliches Piano-Multisample aus, nämlich das frei erhältliche „Salamander Grand Piano“ von Alexander Holm. Hier finden wir angefangen vom tiefen A jede dritte Taste eines Flügels in 16 Dynamikstufen abgesampelt, hinzu kommen jede Menge Extras wie Release- und Pedalgeräusche, die uns im Rahmen dieser Forschungsexpedition aber nicht weiter interessieren sollen. Als Anschauungsobjekt soll uns das C2 in Velocity-Stufe 9 dienen, das wir oben bereits einmal zerlegt hatten:
Das Instrument der Fourieranalyse
Nun, da das Material beschafft ist, stellt sich die Frage nach dem geeigneten Werkzeugkasten. Insbesondere wollen wir uns ein Verfahren konstruieren, um Obertöne zu verschieben. Wie kommt man an diese überhaupt heran? Hierzu verwenden wir das Instrument der Fourieranalyse bzw. -transformation, die in den meisten Programmiersprachen mit gut ausgestatteter Numerikbibliothek standardmäßig verfügbar ist. Sie verwandelt ein auf der Zeitachse gegebenes periodisches Signal p(t) (der vom Mikrofon zu bestimmten Zeitpunkten gemessene Luftdruck) in seine Sinus- und Cosinusbestandteile verschiedener Frequenzen um:
Es können prinzipiell beliebig hohe Frequenzen enthalten sein, der Index k bei beiden Summen läuft bis ins Unendliche und zu jeder Frequenz verraten uns die Koeffizienten ak und bk die Koeffizienten der zugehörigen Cosinus- und Sinusanteile für die k-te Frequenz. Bei digital abgetasteten Signalen ist allerdings bei der Nyquistfrequenz (halbe Abtastrate) Schluss.
Aus Faulheit (im Mathematikerjargon auch „Eleganz“ genannt) werden nun üblicherweise noch die Amplituden ak und bk zu einer gegebenen Frequenz in einer einzigen komplexen Zahl ck zusammengefasst: der Cosinus im Realteil und der Sinus im Imaginärteil.
Mit der inversen Fouriertransformation erhält man dann aus dem Frequenzspektrum dann wieder die Zeitdarstellung, also den Luftdruck als Funktion der Zeit.
Hier ist eine sehr anschauliche Animation dieses Dualismus zwischen Zeitraum und Frequenzraum, von Lucas Barbosa bereitgestellt unter CC-0 (Public Domain).

Animierte Illustration des Dualismus zwischen Zeit- und Frequenzdarstellung. Veröffentlicht von Lucas Barbosa unter CC-0 (Public Domain)
Das soll an Hintergrund erst einmal genügen. Das Schöne an der Fouriertransformation ist, dass man sie als Werkzeug einsetzen kann, ohne die Mathematik dahinter völlig durchdrungen zu haben. Hier also nochmal in aller Kürze die wichtigsten Punkte:
- Die Fouriertransformation liefert die Amplituden der im Signal enthaltenen Frequenzanteile.
- Weil die Fouriertheorie von periodischen Signalen ausgeht, können nur Vielfache der Wiederholfrequenz abgebildet werden.
- Die kleinste darstellbare Frequenz ist f0=1/Periode. Das entspricht einer Sinusfunktion mit einem Berg und einem Tal je Periode.
- Sinus und Cosinus derselben Frequenz treten in der Regel gemischt auf und werden durch komplexe Amplituden ausgedrückt.
Die Annahme, dass unser Signal wie in diesem Beispiel periodisch ist, trifft in der Praxis natürlich so gut wie nie zu. In der Praxis soll uns das aber nicht daran hindern, Fourieranalysen durchzuführen. Wir schneiden das Signal einfach in Stücke konstanter Länge und analysieren jedes dieser Scheibchen so, als würde es sich bis in alle Ewigkeit wiederholen. Das Ergebnis ist eine zeitliche Abfolge von Frequenzspektren, je Scheibchen eins: ein „Spektrogramm“. Sicherlich hat der Audio-Editor eures Vertrauens auch eine entsprechende Funktion. In Audacity beispielsweise gibt es einen Spektrogramm-Darstellungsmodus, in dem die Teiltöne unseres Klaviers deutlich sichtbar werden. Die horizontale Achse ist die Zeit, die vertikale die Frequenz. Angefangen beim Grundton (ganz unten) sehen wir viele parallele Linien in regelmäßigen Abständen, jede eine Harmonische von C2. Man sieht auch einige andere Dinge – zum Beispiel, dass die höheren Frequenzen (durch Reibungsverluste) schneller abklingen als der Grundton.
Es zeichnet sich also bereits schematisch ab, wie der (noch zu konstruierende) Oberton-Verbiege-Apparat ungefähr aussehen wird:
1. Fouriertransformation
2. Editieren der Obertöne
3. Inverse Fouriertransformation
Gerade der zweite Schritt gestaltet sich nicht ganz einfach. Gern handelt man sich beim Herumfummeln an Frequenzspektren Phasenverschiebungen ein, die nach der Rücktransformation als Knackser unangenehm hörbar werden. Wenn man aber einige Kleinigkeiten beachtet, ist das Problem aber einigermaßen gut lösbar.
Audio-Signalverarbeitung mit Python für Dilettanten und -onkels
Der Autor dieser Zeilen ist nicht mit einer exorbitanten Aufmerksamkeitsspanne gesegnet und hat sich daher effektive Vermeidungsmechanismen angeeignet, wenn theoretische Tiefen zu ergründen sind. Statt dessen will ich euch einladen, die oben postulierte Hypothese „Mit Moll klingt‘s toll“ gemeinsam in der Praxis zu erproben. Krempelt also die Ärmel hoch, jetzt wird programmiert! Wir brauchen:
- Eine Programmierumgebung unserer Wahl mit geeigneter Numerikbibliothek, Funktionen für die „Fast Fourier Transform“ (FFT und iFFT) sowie die Möglichkeit zum Lesen und Schreiben von Audiodateien.
Ich habe das hier beschriebene Verfahren zunächst in MATLAB getestet, dann mit Python nochmal nachgebaut. Beide sind mit allem ausgestattet, was wir brauchen; letztere ist kostenlos erhältlich und es gibt viele komfortable Möglichkeiten, sie in Webumgebungen (Notebooks) einzubinden. Mit einem Google-Account kann man über Google Drive sehr bequem loslegen.
- Um die Eingabedaten haben wir uns ja schon gekümmert.
Die Programmierumgebung
Wir fangen an, indem wir in Google Drive ein neues Objekt anlegen, und zwar vom Typ „Google Colaboratory“.
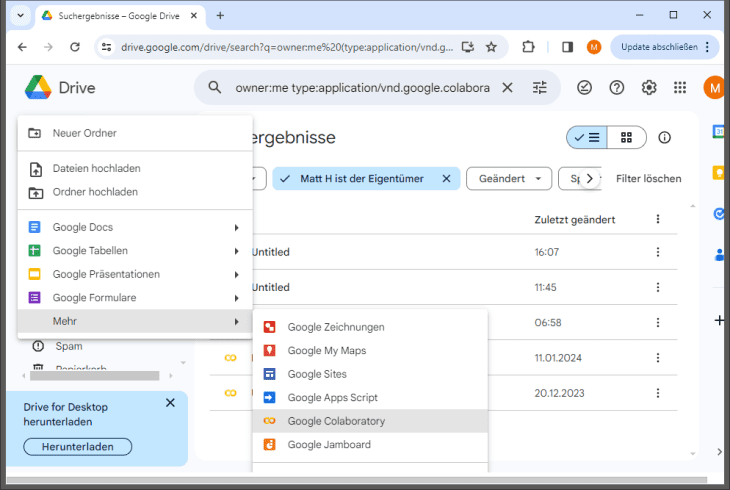 Google Colaboratory – neues Notebook anlegen
Google Colaboratory – neues Notebook anlegen
Öffnen wir dieses, erscheint folgendes Fenster, in dem wir Programmcode in einzeln ausführbaren „Zellen“ organisieren können, und zahlreiche weitere Funktionen zum Verwalten von Daten und Bibliotheken.
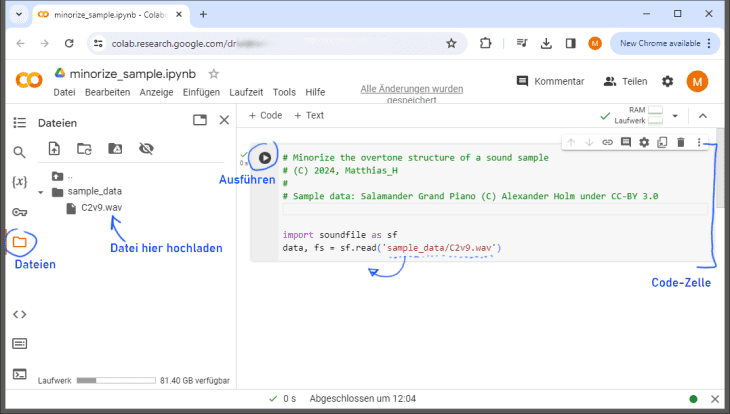
Ein Notebook mit Code- und Ausgabebereich (rechts) sowie einigen Reitern zur Verwaltung von Dateien und Variablen (links).
Unter dem Reiter „Dateien“ befindet sich ein Dateimanager, in dem schon einige Beispieldatensätze liegen. Unser Klaviersample C2v9.wav fügen wir hier via Drag-and-Drop dem Ordner sample_data hinzu. Wer auf die Schnelle keine Kopie findet: hier ist eine. Achtung: auf diese Weise hochgeladene Dateien sind flüchtig und gehen beim Schließen des Notebooks wieder verloren. Aber so eine Datei ist ja im Zweifel schnell wieder hochgeladen. Wie ihr seht, habe ich auch schon ein wenig Programmcode eingefüllt (der, wie bei Google-Dokumenten üblich, ständig gespeichert wird und daher auch beim Schließen erhalten bleibt). Kopiert den folgenden Code in die erste Zelle eueres Notebooks:
import soundfile as sf # Sounddateien lesen und schreiben data, fs = sf.read('sample_data/C2v9.wav')
Es soll demnach die Bibliothek soundfile unter dem Kürzel sf geladen werden; anschließend lesen wir mit der darin enthaltenen Funktion sf.read(…) die WAV-Datei ein.
Nun führt die Zelle per Knopfdruck oder Shift+Enter aus. Es passiert zunächst einmal: nichts. (Statt nichts könnte ggf. auch ein Fehler auftreten, nämlich wenn die Datei unauffindbar ist. In diesem Fall überprüft bitte nochmals den Dateipfad im Code, und dass die Datei auch wirklich an der richtigen Stelle liegt.)
Bei näherem Hinsehen finden wir einen kleinen Haken, der anzeigt, dass der Code dieser Zelle ohne Fehler ausgeführt worden ist. Wie ich mich dann in der „Variablen“-Ansicht vergewissern kann, sind zwei Variablen angelegt worden: die Sampledaten als zweidimensionales Array data (Anzahl der Samples mal Anzahl der Kanäle), sowie die Abtastfrequenz fs. Es handelt sich um eine Stereo-Datei mit 48kHz Abtastate und einer Länge von 1069602 Samples.
Nun, da das offenbar funktioniert hat, lasst uns noch eine Reihe weiterer Bibliotheken laden, die wir später noch brauchen werden. Ersetzt den gesamten Code der Zelle durch diesen hier:
import soundfile as sf # Sounddateien lesen und schreiben import numpy as np # Numerik Grundfunktionen import numpy.fft as fft # FFT und iFFT import matplotlib.pyplot as plt # Grafikausgabe from IPython.display import Audio # Soundausgabe data, fs = sf.read('sample_data/C2v9.wav') num_channels = data.shape[1] num_samples = data.shape[0] Audio(data.transpose(), rate=fs, autoplay=True)
und führt die Zelle wieder aus. Nun sollte ein kleiner Audioplayer erscheinen, der die Datei auch gleich abspielt. Nebenbei haben wir uns die Länge und Kanalzahl in eigene Variablen herausgeschrieben.
Daten verarbeiten
Als nächstes wollen wir die Audiodaten verarbeiten und in eine neue Datei zurückschreiben. Hierzu setze ich euch erst mal einen größeren Brocken Programmcode vor (bitte keinen Schreck bekommen), den ihr gerne 1:1 in eine neue Zelle kopieren könnt. Wer schon einmal programmiert hat, wird sofort Bescheid wissen; für alle anderen habe ich hoffentlich genügend Klartext-Kommentare hinzugefügt, dass die wesentlichen Schritte klar werden. Kurz gesagt, unterteilen wir das Signal, das in der Variable data vorliegt, in Schnipsel konstanter Länge (Fenster) und fügen diese anschließend wieder in data_out zusammen. Wieviele solcher Fenster wir brauchen, hängt von der gewählten Fenstergröße (hier: 512) und der Länge des Audiomaterials ab. Ein eventuelles unvollständiges Fenster ganz am Ende könnte man, wenn man den unbedingt wollte, noch mit Nullen auffüllen. Wir werfen es statt dessen einfach weg, indem wir die Anzahl der Fragmente auf die nächstkleinere ganze Zahl runden. Der Schaden ist überschaubar – 512 Samples bei 48kHz entspricht ein paar Millisekunden an Schall. Bei einem Klavierton, der bereits 20 Sekunden lang ausgeklungen ist, sollte sich der Verlust eines halben Fensters also einigermaßen verschmerzen lassen.
window_size = 512; # Anzahl der Fragmente num_fragments = int(num_samples / window_size) # Ausgabevariable initialisieren data_out = np.zeros([num_fragments*window_size,2]) for ch in range(num_channels): # für alle Kanäle: for i in range(num_fragments): # prozessiere alle Fragmente # Fragment aus dem Eingabe-Array holen frag_in = data[i*window_size:(i+1)*window_size,ch] # Fragment unverändert übernehmen frag_out = frag_in # Ins Ausgabe-Array zurückschreiben data_out[i*window_size:(i+1)*window_size,ch] = frag_out # und schließlich alles zurück in eine Datei schreiben sf.write('sample_data/C2v9_out.wav',data_out,fs,'PCM_24') # Ausgabe über Mediaplayer Audio(data_out.transpose(),rate=fs, autoplay=True)
Eine Python-Besonderheit ist das Indizieren von Arrays mit Teilbereichen (ranges). data[a:b] liefert ein Teilarray, welches Elemente mit Index a bis b-1 aus data enthält. Die Zählung beginnt bei Null, aber auch negative Indizes sind erlaubt. data[-1] bezeichnet das letzte Element des Arrays, data[-3] das drittletzte und so weiter. Das werden wir später noch brauchen, um an die negativen Frequenzen zu gelangen. Zu beachten ist auch, dass die Zeile
# Fragment unverändert übernehmen frag_out = frag_in
nicht etwa die Daten kopiert (deep copy), sondern die Variable frag_out nur als Referenz auf frag_in anlegt. Da kann man fies hinfallen, wenn man an einer Variablen herumoperiert und dabei versehentlich die andere verändert. Nachdem ihr auch diese neue Zellen ausgeführt habt, sollte im Dateimanager eine neue Datei auftauchen. Ladet sie herunter und hört sie euch an. Mit etwas Glück erklingt wieder das vertraute C2 vom Klavier. Falls nicht, könnte es an einer inkonsistenten Einrückung der Zeilen liegen. Programmblöcke, Schleifen usw. werden in Python durch Leerzeichen bzw. Tabs am Zeilenanfang ausgezeichnet. Andere Sprachen verwenden deutlicher sichtbare Syntax wie begin…end oder Klammern {}. Ein weiterer klassischer Fallstrick für die armen Python-Neulinge.
Kurzzeit-Fouriertransformation (STFT)
Warum haben wir uns nun die Mühe gemacht, das Signal erst zu zerstückeln und anschließend wieder zusammenzufügen? Wir hätten es ja schließlich auch gleich in einem Rutsch verarbeiten können. Nun, der Grund hierfür liegt in einer Eigenschaft der diskreten Fouriertransformationen (so auch der FFT), bei der die Länge des Fensters starr an die Auflösung der Frequenzbänder gekoppelt ist. Wir hatten oben ja schon festgestellt, dass wir unsere Frequenzspektren in Vielfachen der fensterspezifischen Grundfrequenz erhalten, also der Sinuswelle, die genau einmal in die Fensterlänge hineinpasst. Im Fall unserer Fensterlänge von 512 wäre diese:
print('Fourier-Grundfrequenz: {:5.2f} Hz'.format(sf/window_size))
Ausgabe:
Fourier-Grundfrequenz: 93.75 Hz
Suchen wir nun etwa nach der Frequenz 187.5 Hz (= 2 * 93.75 Hz), wüssten wir, dass wir diese dank der fixen Fenstergröße immer im 2. Frequenzband finden. Dies wäre beispielsweise nicht der Fall, wenn wir das komplette Audiosignal in ein Fenster packen, dessen Länge dann je nach Sample ja immer eine andere wäre. Auch wenn wir noch nicht genau wissen, an welche Frequenzen wir überhaupt heranmüssen: unser Eingabesample ist ein C2, entsprechend einem Grundton von 65.4 Hz bzw. einer Periode von ungefähr 734 Samples. Lasst uns daher im Folgenden lieber auf eine window_size von 734 wechseln. Und nun laufen wir mit diesem Fenster also über die Audiodaten und können für jedes Scheibchen das Frequenzspektrum berechnen. Wo wir in der inneren Schleife bisher einfach nur kopiert haben:
# Fragment unverändert übernehmen frag_out = frag_in
transformieren wir jedes Scheibchen nun einmal in die Frequenzdarstellung und dann gleich wieder zurück:
# Fouriertransformation spec = fft.fft(frag_in) # [hier wird später die Wurscht gemacht] # Rücktransformation frag_out = np.real(fft.ifft(spec))
Überprüft am besten gleich wieder, ob die Audiodaten noch intakt sind. Der Klavierklang hat es nun immerhin schon einmal überlebt, einmal in den Fourierraum und wieder zurück transformiert zu werden. Die Frage ist nun: was finden wir im Frequenzspektrum spec vor und wie können wir es manipulieren?
Orientierung im Fourierraum
Zunächst einmal, o Schreck, hat das Fourierspektrum spec zwar die gleiche Länge wie das Eingabefragment, aber wir erinnern uns: Fourierkoeffizienten kommen als komplexe Zahlen daher. Auch wen wir das jetzt von der mathematischen Seite her nicht komplett durchdringen können, ist aber wichtig zu bedenken, dass es in der Fourier-Welt positive und negative Frequenzen gibt. Nur wenn ich die paarweise zusammen anfasse, kann ich (bis auf Rechenungenauigkeiten) sicherstellen, dass ich nach der Rücktransformation keine komplexen Zahlen herausbekomme. Außerdem sind, wie wir bereits wissen, sind die im Fourierspektrum aufgelösten Frequenzbänder ganzzahlige Vielfache der FFT-Grundfrequenz. Konkret auf unser spec bezogen, finde ich das n-te Frequenzband an der Stelle spec[n] und die dazugehörige negative Frequenz an der Stelle spec[-n], also im n-t-letzten Element des Arrays. spec[0] ist die DC-Komponente, also der konstante Anteil. Als erstes Experiment könnten wir uns an einem Hochpassfilter versuchen. Wenn wir Frequenzbänder -5 bis 5 auf Null setzen, sollte das doch ungefähr einem Lowcut um 450Hz entsprechen. Probieren wir es doch mal aus:
# Fouriertransformation spec = fft.fft(frag_in) # Manipulation des Spektrums - hier: Hochpassfilter spec[0:5] = 0 spec[-5:len(spec)] = 0 # Frequenzbänder -5 bis -1 # Rücktransformation frag_out = np.real(fft.ifft(spec))
Spielen wir die Ausgabe dieses Codes ab, hören wir in der Tat eine Variante des Pianosamples, bei dem hohe Frequenzen stark gedämpft sind. Ebenfalls zu hören ist aber auch ein ziemlich fieses Gebritzel. Dieses hängt mit der scheibchenweisen Prozessierung des Audiosignals zusammen. Nach Manipulation passen die Fragmente nicht mehr nahtlos aneinander, es gibt Wertesprünge und die sind als Knackser deutlich hörbar. Hier helfen wir uns, indem wir jedes Fragment mit einer linearen “Korrekturrampe” versehen, die den Start- und Endwert auf den alten Wert zurückzieht.
# Zu Reduzierung von Knacksern Anfangs- und Endpunkte anpassen
correction_ramp = np.linspace(frag_in[0]-frag_out[0],
frag_in[-1]-frag_out[-1],
window_size)
# Ins Ausgabe-Array schreiben
data_out[i*window_size:(i+1)*window_size,ch] = frag_out + correction_ramp
Das ist nun sicher noch nicht die ganz hohe Schule der Audiosignalverarbeitung, aber das Britzelproblem bekommen wir damit einigermaßen effektiv in den Griff.
Fazit und Hausaufgaben
So, ihr Lieben – die nötigen Vorarbeiten sind gemacht. Wir verstehen jetzt, warum Mollakkorde einen physikalischen Nachteil gegenüber Durakkorden haben. Und wir haben Material und Handwerkszeug beisammen, um dagegen etwas zu tun. Unter anderem können wir jetzt schon:
- Audiodaten in Python laden,
- diese Daten in Fragmente zerlegen und wieder zusammenfügen,
- Audiodaten in den Fourierraum und zurück in die Zeitdarstellung transformieren und
- einfache spektrale Veränderungen vornehmen.
Während ich Teil 2 dieses Workshops aufschreibe, versucht euch doch auch mal an eigenen Manipulationen. Zum Beispiel könntet ihr ein Tief- oder Bandpassfilter implementieren oder Frequenzanteile im Spektrum herumschieben. Probiert auch mal aus, was mit Fenstergröße 512 klingt – es funktioniert schon alles deutlich besser, wenn das Analysefenster aufs Tonmaterial angepasst ist. Ganz Mutige dürfen sich auch gerne schon einmal an der Mollifikation versuchen – fairerweise sei hier aber verraten, dass wir vorher noch ein klein wenig mehr rechnen müssen. Einstweilen hier schon einmal mein eigenes Ergebnis als Amuse-Gueule:
Nun seid ihr dran – tobt euch aus und berichtet in den Kommentaren von eueren Ergebnissen. Ich freue mich auf eure Rückmeldungen!








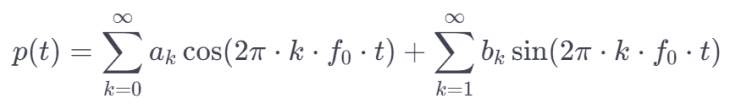


Errata, Vol. 1 (ich kann den Artikel hier leider nicht mehr editieren):
* Der Titel „Workshop Harmonielehre“ stammt nicht von mir. Es geht um einen Programmierworkshop in Python zwecks Manipulation von Obertonspektren.
* Anstatt händisch mit der Eingabedatei herumzufummeln, kann man sie auch automatisch herunterladen lassen, indem man ganz oben in der ersten Zelle ergänzt:
# Lade C2v9.wav aus dem Salamander Grand Piano, © Alexander Holm unter CC-BY 3.0
!wget -nv -O sample_data/C2v9.wav „https://drive.google.com/uc?export=download&id=1EuMzd0oQadc0bjrzTK50PYHPddzBT4fX“
* Im Hochpassfilterbeispiel muss es zur Entfernung der ersten 5 Teiltöne korrekt heißen (Zeilen um je 4 Leerzeichen eingerückt):
# Manipulation des Spektrums – hier: Hochpassfilter
spec[0:6] = 0
spec[-5:] = 0 # Frequenzbänder -5 bis -1
* Im darauf folgenden Text müsste es korrekt heißen, dass statt den hohen Frequenzen die *tiefen* gedämpft sind.
* Die Links ganz unten sind kaputt. Hier müsst ihr die URLs in einen anderen Tab copy-and-pasten.
Hallo Matthias,
der Titel Deiner Story enthält ja schon diesen augenzwinkernden Begriff „alternative Universen“.
Wie Du richtig beschreibst, bestimmt die Physik und Naturgesetze die Reihenfolge der Harmonischen – ich verkneife mir hier mit Rücksicht auf die Umgangsformen im Forum gerade beim Begriff „Gesetze“ etwas Klischee-behaftete Seitenhiebe …
Die klangliche Beschreibung der Wirkung von Dur und moll ist individuell unterschiedlich. Ich verwende sprachlich für moll eher den Begriff „angespannt“, für Dur als Gegensatz dazu „gelöst“ und „harmonisch“; letzteres resultiert eben aus der natürlichen Reihenfolge der Harmonischen.
Optisch helfen mir mit Blick auf die Klaviertastatur dagegen die Begriffe „eng“ für moll und „weit“ für Dur. Diese Betrachtung hat mir auch sehr dabei geholfen, mir autodidaktisch das Spielen von Tonleitern (Ionisch Dur und Äolisch moll) auf einer Klaviatur für alle Töne einprägsam beizubringen.
Unten weiter mit Teil II (wg. begrenzter Anzahl Zeichen)
@NDA Teil II:
Ich hab‘ hier zwar selber einen Artikel zur Abfolge von Harmonischen & Intervallen verfaßt (link: https://www.amazona.de/community/harmonielehre-intervalle-harmonische-und-frequenzverhaeltnisse/), verweise an der Stelle aber gerne auf Wiki, da sie den wesentlichen Punkt dort im Kapitel „Tastaturbelegungen als Vorlage“ (link: https://de.wikipedia.org/wiki/Tonleiter) sehr schön darstellen. „Eng“ und „weit“ ergibt sich damit aus der Abfolge der charakteristischen Terzen und vor allem mit Blick auf die gesamte (!) Tonleiter:
Äolisch moll beginnt mit der kleinen Terz. Vom 3. auf den 4.Ton ist es ein Halbtonschritt, der die Basis für die nächste, wiederum kleine Terz ist. Deren letzter Ton (6.) bildet eine große Terz rauf zur Oktave. Also zwei kleine Terzen in Folge. Bei moll ist es beginnend vom Grundton sowohl die kleine Terz als auch die kleine Sexte, die diesen auch optisch „engen“ Charakter verursacht. Die ganzen Reibungen kommen von diesen „speziellen“ Halbtonintervallen und spielen sich vor allem in den Obertönen ab (kommt vermutlich in einer weiteren Folge Deines Artikels).
Ionisch Dur ist dagegen komplett umgekehrt: Große Terz; wieder Halbtonschritt von 3. nach 4., gefolgt von der nächsten großen Terz. Vom 6. Ton dann aber die kleine Terz rauf zur Oktave. Somit erst zwei große Terzen in Folge – also ein großer, „weiter“ Schritt vom Grundton zur (großen) Sexte.
@NDA Hätte ich von deinem Artikel doch früher gewusst! Dann hätte ich einfach im Text darauf verwiesen und hätte viel schneller auf den Punkt kommen können.
Dass eine Molltonart nicht nur aus dem Grunddreiklang besteht, ist völlig korrekt. Soviel sei zum nächsten Teil schon verraten: nur mit einem einheitlich „mollifizierten“ Obertonspektrum kommen wir nicht weit und es klingt tatsächlich sogar ziemlich bescheiden. Um Musik in einer Molltonart machen zu können, braucht man zumindest für alle 12 Halbtonstufen darüber die passenden Dreiklänge, die dann je nachdem entweder Moll, Dur oder vermindert sind. Da werden wir also noch einiges basteln müssen, damit es am Ende passt.
@NDA …und dazu die altmodischen Deutungen „hart“ und „weich“ (vom Italienischen), die sich bis heute hartnäckig im Notennamen „H“ halten 🙂
An den Autor: total spinnerte Idee, aber hey, warum nicht? Was passiert eigentlich, wenn ich mit nem kompletten Mollklavier so klassische Literatur wie, sagen wir, Bach, oder späten Beethoven, oder Stockhausen, oder Strayhorn, oder Mercury spiele?
… wollte ich gerade schreiben, bis ich den letzten Kommentar von @MatthiasH las. Aber die Frage bleibt: nicht nur beim späten Beethoven sondern auch bei Jobim oder so bin ich ja selten reinrassig dur oder moll..
@moinho Moin Ho,
jetzt kommst Du auch noch mit diesem leidigen „H“ – ein weiterer Stolperstein auf meinem traumatischen Weg Struktur in diese ganze Musiktheorie hineinzubringen…
… aber Halt! – ist das vielleicht sogar die geniale Eselsbrücke, um die a-moll / C-Dur Verwandschaft hervorzuheben: a Ha! C – kleine( r ) T(sch)erz! 😂
OMG, dagegen verblaßt der englische Pragmatismus von wegen A B C natürlich völlig …
Ich geh‘ besser schlafen, ist schon spät … 😉
Vielen Dank für den interessanten Ansatz. Bin gespannt, wie sich das weiter entwickelt.
Wer kein Klavier zur Hand hat: es gibt auf YT einen kurzen Film der die Obertonreihe am Klavier erklärt: „Die Obertöne am Klavier“
@Autarkus Man kann natürlich auch eine Trompete nehmen :-)
Nach (zugegebenermaßen oberflächlicher) Lektüre des Artikels fällt mir folgendes ein:
1. „Du mußt doch gut in Mathe sein, immerhin machst Du Musik.“ (meine Musiklehrerin in 13/I). Ich stand auf einer glatten Fünf in Mathe, und bin noch heute stolz darauf.
2. „Ich bin doof, ich mach Musik.“ (Aufkleber, der einst einer Ausgabe des Fachblatt Musikmagazin beilag).
Spätestens beim Formelwerk war ich raus.
Haha, lass dich von sowas bitte nicht abschrecken. Die Formeln sind nur ein kleiner visueller Flex, tatsächlich handelt es sich bei den großen griechischen Sigmas um nichts anderes als „Plusrechnung“. Im Klartext steht da also: „Addiere unendlich viele Sinus- und unendlich viele Cosinuswellen“.
@MatthiasH Das sagst Du so.
Ich habe keinen Draht zu Formeln und Theorien. Ich habe Schach nie verstanden, weil ich so nicht denke. Das ist kein intellektuelles Problem, sondern einfach tiefverwurzeltes Desinteresse an Naturwissenschaften und ihren Gesetzmäßigkeiten. Bei meiner Chemielehrerin habe ich mit der Bemerkung, daß ich das alles für ziemlich willkürlich konstruiert und nicht nachvollziehbar halte, nicht wirklich beliebt gemacht. Ein Schulfreund von mir spann den Faden weiter und meinte, er würde das Periodensystem höchstens nach dem Eisprung seiner Freundin berechnen…
Ich habe Synthesiser und ihre Funktionsweise auch nicht durch Wolfgang Bocks Buch „Synthesizer“ verstanden (das war mehr so die Abteilung „Ich erkläre Musik mit Lötzinn“), sondern nur dadurch, daß ich wild daran herumgedreht habe — ich arbeite lieber von der Praxis in die Theorie, nicht umgekehrt. Wie das dann als Formel aussieht…
Bin halt kein Wissenschaftler.
Es muss jeder seinen Zugang finden. Was @NDA oben abzieht, ist mir persönlich schon wieder zu verkopft, ich finde kaum etwas schwieriger als Unterhaltungen mit Leuten, die über Musik theoretisieren, ohne die passenden Tonbeispiele zur Hand zu haben. Mein Ansatz zielt daher meist in Richtung „20% kapieren, 80% Ergebnis“.
Schön daß es mehr so Leute gibt. Ich habe in 13/I erst Mathe abwählen können, weil ich zu wenig Punkte hatte. Das war ein Krampf. Bin froh als ich es los war, habe noch Jahre danach davon geträumt, eben ein echtes Trauma. 😄
@Kazimoto Eine Fünf in Mathe kommt einem Purple Heart auf dem Schlachtfeld gleich:
Damit kann man sich voller Stolz schmücken.
Ob es dafür unbedingt eine Schlacht brauchte, steht auf einem anderen Blatt.
Interessanter Ansatz. Was kriegt man denn für „nicht kochen können“? 😘
@MatthiasH Im Zweifelsfalle nichts Gescheites in den Magen.
Hier gibt es nix zu sehen.
Alle Jahre wieder kommt irgendwer angetanzt und meint er hätte ein „besseres Piano“ erfunden das angeblich fundamentale Probleme löst und dann klingts wie Grütze. ;)
@plumperquatsch Hast du den Account eigentlich nur angelegt, um hier herumzutrollen? Außer dir haben es alle irgendwie geschafft, ihren Tonfall respektvoll zu halten – auch wenn sie mit den Inhalten nichts anfangen können und/oder sonst eher ein ruppiges Image pflegen.
Wenn du schon so offensichtlich nicht das geringste Interesse an „was wäre, wenn“-Experimenten hast, vergifte doch bitte wenigstens nicht die Atmosphäre für diejenigen, die sich neugierig bzw. ergebnisoffen darauf einlassen wollen.
@MatthiasH Wenn ein Instrument den Test der Zeit bestanden hat dann das Piano.
Finger weg.
Da haben sich schon ganz andere Leute mit ihren Experimenten die Finger dran verbrannt. ;)
@plumperquatsch Nach dem, was du hier bislang an Substanz eingebracht hast (vor allem Beleidigungen und Zwinkersmilies), fällt es mir schwer, dich in dieser Sache als Autorität anzuerkennen.
Denkfehler:
was ich als harmonisch oder dissonant wahrnehme hat überhaupt nichts mit der Physik hintendran zu tun, (!)
sondern beruht ausschließlich auf Prägung/Hörgewohnheiten/in welchem Kulturkreis bin ich aufgewachsen. ;)
Was sich für mich anhört als wäre die Milch sauer geworden kann für eine andere Person ganz toll harmonisch sein und Verzückung auslösen.
@plumperquatsch Überhaupt kein Denkfehler, richtig und wichtig sind natürlich beide Faktoren!
Klar spielen Hörgewohnheiten eine immense Rolle und dominieren vermutlich alles andere.
Aber bei der Frage nach dem Wohlklang von Intervallen ist tatsächlich handfeste Physik/Mathe im Spiel. Dabei spielt nicht nur das Frequenzverhältnis eine Rolle, sondern auch die absolute Tonhöhe, Bei der Addition zweier Töne entsteht – mathematisch dasselbe wie wenn man einen Ton (die Summe der beiden Einzelfrequenzen) amplitudenmoduliert mit dem Differenzton. Das nennt man Schwebung, und bei der Frage nach dem Wohlklang ist von entscheidender Bedeutung, ob diese Schwebungsfrequenz im hörbaren Bereich liegt (dann wird sie einfach als weiterer Ton oder gar nicht wahrgenommen) oder im Infraschall, dann höre ich Lautstärkeänderungen, also irgendwas zwischen schnellem Flattern und langsamem Wabern. Daher klingen im tiefen Bass selbst Terzen und Quarten ziemlich schlimm, während du bei hohen Tönen (und einer gewissen Jazz-Sozialisation ;-)) gelegentlich auch mit kleinen Sekunden durchkommst.
@MatthiasH „Aber bei der Frage nach dem Wohlklang von Intervallen ist tatsächlich handfeste Physik/Mathe im Spiel.“
nein.
„wohlklang“ ein Kulturkonstrukt.
kann ich als schön, unschön oder meh empfinden.
vielleicht mag ich die Stimmung nach Pythagoras, vielleicht nicht.
vielleicht mag ich die wohltemperierte Stimmung, vielleicht nicht.
vielleicht ist mir das alles unangenehm und ich mag *insert something exotic here* Gamelan Orchester.
@plumperquatsch OK, dann sehe ich keinen Sinn in einer weiteren Auseinandersetzung über dieses Thema und wünsche noch einen schönen Tag.
@plumperquatsch Das ist kommunistisches Geschwurbel welches ich ganz einfach widerlegen kann, da ich mir ziemlich sicher bin mit Hilfe der Physik Töne und Klänge herstellen zu können, die in allen Kulturkreisen als schrecklich empfunden würden. Z.B. einenen 440 Hz Ton bei 300 db Spl
Jeztzt höre ich bei jedem tiefen Klavierton die große Terz in den Obertönen bewusst.
Bin ich für Moll für immer verloren?
Du bist schuld, MatthiasH!
@bluebell Nicht nur für Moll, auch für Dur bist du verloren ;-) Nimm mal C-Dur mit E im Bass, dann kriegst du oben ein dickes fettes fieses Gis ins Gehege.
Zum Glück können sich unsere Ohren (bzw. das Hirn dazwischen) ja an einiges gewöhnen.
Notes and Neurons: In Search of the Common Chorus
https://www.youtube.com/watch?v=S0kCUss0g9Q
@plumperquatsch Danke für das Gegenbeispiel zu deinem obigen Argument ;-) Gerade die Pentatonik als gemeinsamer Nenner der allermeisten Musikkulturen zeigt doch sehr deutlich, dass sich Hörgewohnheiten auch nicht x-beliebig entwickeln. Die zu Grunde liegenden Faktoren sind zum Teil kulturunabhängig und naturgegeben.
@MatthiasH naja, die pentatonik ist so ziemlich das einfachste worauf man sich einigen kann.
es gibt keine „falschen“ töne ;)
ausserdem ist das Beispiel fragwürdig,
Bobby suggeriert und allen machen nach/mit …
das Publikum hat nur einen ton geraten (den 3.), alles andere wurde vorgemacht.
aber lustig wars.
Ich musste es mir auch mehrmals ansehen um zu verstehen was da passiert. ;)
@MatthiasH Bobby ist ein Profi, der macht so Geschichten ständig.
Was nehmen wir also für die Hör-zu-und-sing-mit-party?
die pentatonik- da kann am wenigsten schief gehen. ;)
@MatthiasH Du hast nicht verstanden was da gesagt & gezeigt wird.
Wenn man die Stimmung gefunden hätte auf die sich alle einigen können, müsste man sie nicht mehr suchen. ;)
In search of …
nicht here´s the thing, its pentatonic.
@plumperquatsch Ich glaube, es wird für dich jetzt Zeit, dich an den Aufschrieb deines eigenen Artikels zu setzen, der ohne Zweifel viel besser sein wird als dieser. Vielen Dank für die Beteiligung an der Diskussion und bis bald.
Egal ob Dur oder Moll – Klaviere und die Obertonreihe stehen in einem sehr angespannten Verhältnis zueinander und das macht auch gerade den vibrierenden Klangcharakter des Instruments aus. Da stimmt einfach nix, nicht mal die Oktaven, Stichwort gespreizte Stimmung. Interessanter wäre das ganze, wenn man tatsächlich Dur und Moll intonieren könnte. Für dieses Experiment Klaviersamples zu verwenden finde ich daher ziemlich seltsam.
@whywebern Fühl dich herzlich eingeladen, x-beliebige andere Samples heranzunehmen! Den Code dafür hast du ja.
@MatthiasH Außerdem steht es dir natürlich auch völlig frei, overtone f*ckery außerhalb jeglichen Harmoniekontexts zu betreiben.
Die Antwort auf die Frage lautet, dass nur die Obertonreihe im Ohr der Hörerinnen und Hörer ‚einrastet‘ und als Klang (statt Akkord) gehört wird, d.h., wenn etwas entfernt wird, entspricht es einer Klangveränderung, und wenn etwas Fremdes (das nicht Teil der Obertonreihe ist) hinzugefügt wird, entspricht es einem Zusatzton.
(Nebenbei bemerkt: Ich bin jedoch der Meinung, dass MusikerInnen sich nicht zwangsläufig um die Obertonreihe kümmern müssen und machen können und vor allem machen sollen was sie wollen ;) )
@Jeanne „wenn etwas entfernt wird, entspricht es einer Klangveränderung, und wenn etwas Fremdes (das nicht Teil der Obertonreihe ist) hinzugefügt wird, entspricht es einem Zusatzton.“
schwierig,
„wenn etwas entfernt wird, entspricht es einer Klangveränderung,“
heißt wenn ich Obertöne lösche bekomme ich ein anderes timbre – so weit so gut
„wenn etwas Fremdes (das nicht Teil der Obertonreihe ist) hinzugefügt wird, entspricht es einem Zusatzton.“
wir nehmen 2 osc und verstimmen einen um ein paar wenige cent,
jetzt haben wir 2 obertonreihen und die Obertöne der einen reihe passen nicht wirklich in die andere obertonreihe (offset)
was wir dominant hören ist eine timbre Veränderung und nicht einen Zusatzton 🤔
darüber lässt es sich schlecht reden,
der definition nach ist alles was nicht pitch ist ist timbre,
aber hier verschwimmen die Definitionen und das eine (pitch) ist von dem anderen (timbre) nicht mehr trennbar; die Verstimmung(pitch) macht das timbre. 🤷🏻♂️
@Jeanne Ganz so eindeutig ist es meiner Meinung nach nicht, siehe Klänge mit anharmonischen Spektren (2D- und 3D-Resonatoren wie Trommeln, Glocken; auf der elektronischen Seite FM, Ringmod usw.) Bei Carillons beispielsweise habe ich nur einen extrem engen Sweetspot, wo ich überhaupt den „intendierten“ Ton höre. Es darf nicht zu laut und nicht zu leise sein, die Quelle darf nicht zu nah und nicht zu weit weg sein, und so weiter
Zur Maxime „tu worauf du Bock hast“: 100% Zustimmung 😄
„Ein C im Bass schafft also klare Fakten in Richtung C-Dur.“
nein.
a-moll passt auch sehr gut. ;)
@plumperquatsch Sag ich doch: C-Dur ;-)
@MatthiasH Mit a-moll vs. c-dur kann ich mich den halben Abend lang amüsieren. 😁
Der oben erwähnte Herr Beethoven hatte da auch keine Probleme.
Oh, ich kann die mondscheinsonate nicht in gis moll schreiben, da hab ich esoterische Probleme. ;) 😆
@plumperquatsch Zur Mondscheinsonate kommen wir noch. Da gibt es viel zu entdecken.
Immer wieder spanndend, auf welchen Wegen man sich der Musik nähern kann!
Auch wenn es mir irgendwann zu hoch – oder tief – wurde, freue ich mich auf die Fortsetzung und bedanke mich fürs Teilen!
Ein cooler Artikel, der sich dem Thema Musik zur Abwechslung aus physikalisch-technischer Sicht nähert und dabei zugänglich bleibt.
Ich finde Datenprojekte mit Python auch ohne Musikbezug spannend und fand ihn daher besonders spannend. Dass Google auch Notebook-Funktionalität bereitstellt, wusste ich bisher noch gar nicht.
Freue mich jedenfalls auf den zweiten Teil!
Hallo Matthias,
Respekt und Danke fuer die Story und Arbeit die da drin steckt.
Nach jedem Absatz den ich gelesen und nicht verstanden habe, hab ich mich ans Klavier gesetzt und Beethoven gespielt.
Hier wird gerade viel Beethoven geübt… Danke.. 😂
Nachm ersten Takt der Pathentique gings mir wieder besser.
C-moll ist einfach nur geil. 😁
Vielen Dank Mathias für den sehr interessanten Workshop und bitte nicht allzu lange am Kliff hängen lassen. Finde die Idee den experimentellen Ansatz und die wissenschaftliche Methode auf das Thema anzuwenden sehr schön. Und um so besser sich selbst und anderen die Angst vor den vermeintlich komplizierten Hintergründen zu nehmen in dem man das ganze einfach mal zusammenschustert. Kommt in Folge 3 auch noch das ganze auf Echtzeit zu optimieren? Das wär‘s.
@sparsepix Hallo, lieber Freiwilliger! :-) Wenn du willst, versuch doch mal, ob die Library PyAudio in dieser Cloud-Umgebung funktioniert, die kann (angeblich) Echtzeit I/O – auch wenn ich es selbst noch nicht ausprobiert habe. Bei Fourier bekommt man natürlich immer mindestens die Fensterlänge als zusätzliche Latenz.
Noch a Idee, nämlich additive Synths.
Da gibts esoterische Oszillatoren im Modularuniversum – und alte und ganz alte Polys.
K5000: pro Stimme 2 Oszillatoren, die je 32 Partialtöne machen, wobei der Haken ist, daß die harmonisch sind (ansonsten krieg ich für jeden ne riesige Hüllkurve und so).
Also könnte ich den „Klang ohne die großen Terzen“ mit einem Oszi bauen (und akzeptieren, daß nach nr. 32 Schluß ist), und den anderen für die großen Terzen verwenden. Hmmm…
@moinho Du meinst das Klavier im K5000 nachbauen? Leider ist ja bei 32 Teiltönen noch lang nicht Schluss, gerade die tiefsten Töne klingeln obenherum noch weit darüber hinaus. Und dann noch für jeden Oberton die passende Hüllkurve programmieren, viel Spaß.
Auch mein simples Framework kann man natürlich in Richtung Synthese ausbauen; der Fourier-Umweg mit seinen doofen Fensterübergängen macht es einem aber nicht gerade leicht. Ich fummle hier ja nun schon seit geraumer Zeit herum und eine präzise Kontrolle über die Phasenrelationen ist generell in weiter Ferne – es knackst und rumpelt doch an allen Enden.
Daher hier mein Vorschlag: lass uns doch lieber komplett analog bleiben und die 92 oder wieviel Sinuskomponenten einer hierzu eigens umgebauten Tonewheel-Orgel mit der passenden Filterbank ansteuern 😄
@MatthiasH
Ich möchte mich für Deinen enorm interessanten Beitrag bedanken!
Selbst begann ich mich vor zwei Jahren mit der Harmonielehre generell und der diatonischen Stammtonleiter im Speziellen zu beschäftigen. Schwerpunkt ist die Visualisierung tonaler Harmonik. Eine der ersten Besonderheiten für mich waren, dass die 7. und die 13. Harmonische (Naturseptime & Alphorn-Fa) allgemein als Dissonanzen aufgefasst werden – nebst dem bekannten Moll-Problem.
Hierbei war es einerseits die Arbeit von Prof. Martin Ebeling, welche von den neuronalen Prinzipien hinter der Wahrnehmung von tonaler Konsonanz handelt und tatsächlich so etwas wie eine gewisse biologisch determinierte Universalie hinsichtlich harmonischer Empfindung beschreibt (Link siehe unten). Also fundiert darlegt, weshalb „unsere“ Tonleiter so populär geworden ist.
Und bezüglich des Moll-Problems war es hilfreich, die dezimale Repräsentation von Intervallen zu betrachten. Die (phrygisch reine) kleine Terz (6/5 also 1,2), kleine Sexte (8/5 also 1,6) sowie kleine Septime (9/5 also 1,8) ergeben jeweils ein Zehntel einer Dur-Harmonischen. Nämlich der Quinte (12), Oktave (16) und Sekunde (9). Und nur Quinte & Sekunde stehen in der Stammtonleiter in quadratischer Beziehung; nämlich 9/8 & 3/2. Damit lässt sich gut arbeiten.
Viele Grüße :-)!
https://www.lehmanns.de/shop/mathematik-informatik/7802277-9783631561027-verschmelzung-und-neuronale-autokorrelation-als-grundlage-einer-konsonanztheorie
Als Physiker habe ich ja großen Spaß an solchen Experimenten 👍
Bevor ich mich an die Beantwortung der Ausgangsfrage „Klingen Moll-Tonarten besser bzw. konsonanter, wenn das Obertonspektrum des verwendeten Instruments ebenfalls in Moll ist? Intuitiv könnte man ja meinen, dass sich die Teiltöne dann besser vertragen und der Gesamtklang harmonischer wird.“ gemacht hätte, hätte ich allerdings erstmal eine viel einfacher zu beantwortende Frage überprüft: „Wirken Moll und Dur anders, wenn man reine Sinustöne verwendet?“ Das lässt sich leicht mit jedem sinusfähigen Synthesizer in Sekunden ausprobieren. Nach meinem Empfinden: Nein, für mich klingt ein Moll-Akkord aus Sinustönen nicht weniger ‚mollig‘ als mit Sägezähnen oder Pianosamples gespielt.
Trotzdem natürlich ein sehr spaßiges Projekt 🙂
@MatthiasH
ein sehr interessanter Beitrag, bin gespannt auf die Fortsetzung. Die musiktheoretischen Grundlagen sind mir in groben Zügen klar; auch wenn ich die Mathematik dahinter nicht mehr gänzlich durchdringe, werde ich mich wohl mal an Python versuchen.
Die Idee, das Obertonspektrum eines Grundtons zu manipulieren, stößt bei mir noch aus einem ganz anderen Grund auf großes Interesse: als E-Bass-Spieler hat es mich oft genervt,
dass eine Equalizer-Einstellung, die für den einen Grundton perfekt passt, bei deutlich höheren / tieferen Tönen weniger passend klingt.
Einmal abgesehen von der Beeinflussung des Frequenzgangs durch Verstärker, Speaker etc. habe ich das auch darauf zurückgeführt, dass der eingestellte Klangfilter ja „absolut“ ist und nicht mit dem Grundton „mitwandert“.
Aus deinem Beitrag schließe ich, dass es durchaus auch möglich wäre, einen digitalen „Oberton-Equalizer“ zu entwickeln, bei dem sich die Filter relativ zum Obertonspektrum des Grundtons mit verschieben ….
Wenn es so etwas nicht schon gibt (ich habe als Hobbymusiker den Aufbruch ins Zeitalter der digitalen Klangbearbeitung verpasst).
Und wenn das für die Klangregelung wirklich was brächte….
@Cilph Beim Bass (monophon gespielt) ist das gar nicht mal so abwegig. Man müsste erst einmal den Grundton detektieren (nicht ganz sooo einfach, über schlecht „trackende“ Octaver usw. können die Saitenleute hier ja den Blues singen), und dann darauf basierend filtern. In Echtzeit schwierig und nur mit einiger Latenz zu machen, bei Samples aber natürlich überhaupt kein Problem.
@Cilph Schau dir mal das Harrison XT-BC Plugin an, das macht das so. Ich nutze das manchmal.
Spannender Artikel!
Viele Artikel hier auf amazona befassen sich mit Technik (meist Elektro-, Akustik etc.). Ich frage mich dann oft, ob ich nicht vieleicht in der Zeit zum Instrument hätte greifen sollen. Musik machen statt technisches knowhow aufbauen!
Dein Artikel ist auch technisch, aber für mich ein erfrischend neues Thema! Freue mich auf den nächsten Teil. Und vlt schmeiß ich Python mal wieder an:)
Sehr interessanter Beitrag, ich finde den mathematischen Ansatz sehr Spannend, habe leider nicht alles verstanden aber trotzdem.