Einleitende Worte zur Harmonielehre

Viele der heutigen Musikrichtungen führen zu einem interessanten Aufeinandertreffen von Künstlern (Musiker, aber auch Producer und Mixing-Engineers) und Technik(ern), verbunden mit viel Elektronik dahinter (Instrumente, Recording– und Mixing–Equipment).

Wir alle wissen, daß sich damit wunderbare Musik schaffen läßt.

Aus Musikersicht genügt dem einen dabei das reine Spielen der Instrumente und als Musikhörer der pure Musikgenuß. Andere dagegen sind auch an den technischen Zusammenhängen interessiert; sei es aus reiner Neugier, oder dem Wunsch sie gezielter für die Kreativität nutzen zu können.

Ich mache mir schon länger Gedanken darüber, wie man hier technische & physikalische Inhalte ohne große Theorie anschaulich mit den bekannten Begriffen und Bildern der Musik vermitteln bzw. darstellen und beide Welten so noch näher zusammenbringen könnte.

Viele musikalische Grundlagen sind sicher hinlänglich bekannt, und das schreibe ich nicht nur aus Bequemlichkeit. Sehr oft genügt es ab einem gewissen Wissensstand und Erfahrungen teils „verschüttetes“ Wissen wieder aus den Tiefen des Gedächtnisses auszugraben. Weiter gibt es passend zu diesem Artikel im Forum eine sehr schöne und ausführliche Serie zur Harmonielehre (s. links am Ende) mit vielen Audiobeispielen. Ich mache mir das zu Nutze und lege meinen Schwerpunkt vielmehr darauf, die Zusammenhänge mal ergänzend aus einem etwas anderen Blickwinkel zu beleuchten. Gemäß dem Motto „Viele Wege führen nach Rom“; und auf jedem Weg gibt es etwas zu entdecken.

Zum Einstieg gibt’s eine Auffrischung zum Thema Intervalle, Harmonische und die zugehörigen Frequenzverhältnisse. Idee ist dabei eine Basis und gemeinsame Darstellung zu schaffen für weitere kleine Artikel, die mir so im Kopf schweben:

• Signalformen und ihre Harmonischen / Frequenzzusammensetzung
• Synthesearten
• Filterung, Verzerrung & Modulationen

Das als zusätzliche Betrachtungen zu einigen wirklich guten & empfehlenswerten Workshops und Artikelserien hier im Forum (die links werden jeweils angefügt). Speziell für diesen Beitrag hier möchte ich auf das Buch „Die neue Harmonielehre“ von Frank Haunschild im AMA-Verlag hinweisen [bekomme dafür aber keine Provision ;-)]. Zwar basieren meine Überlegungen aus der eigenen Lernkurve; prinzipiell wird dort jedoch ein vergleichbarer Ansatz zur Erklärung verwendet (allerdings unter Verwendung des „klassischen“ Notationssystems).

Intervalle und „Harmonische“ –

und ein „Einstiegscheck“ für Profis & Eilige

Zeit ist knapp, daher möchte ich die Profis nicht zu lange aufhalten, die das eh alles aus dem Eff-Eff beherrschen.

Wesentlicher Punkt ist die (indirekte) Darstellung der Frequenzen mit Hilfe der  – Musikern bestens vertrauten – Klaviatur an Stelle einer technischen Frequenzskala, um so den direkten Bezug zu Noten und ihren dazugehörigen Frequenzen zu schaffen.

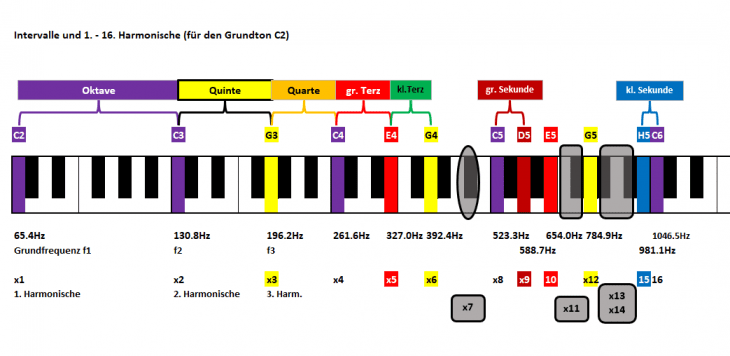
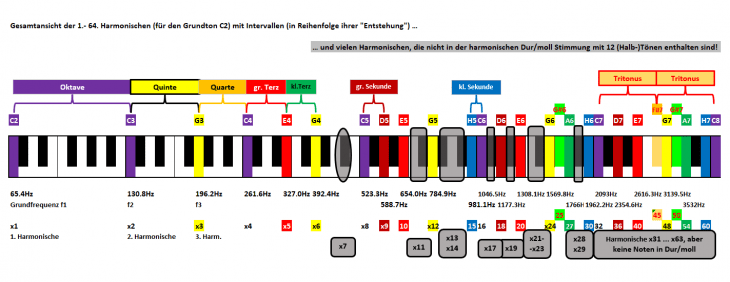
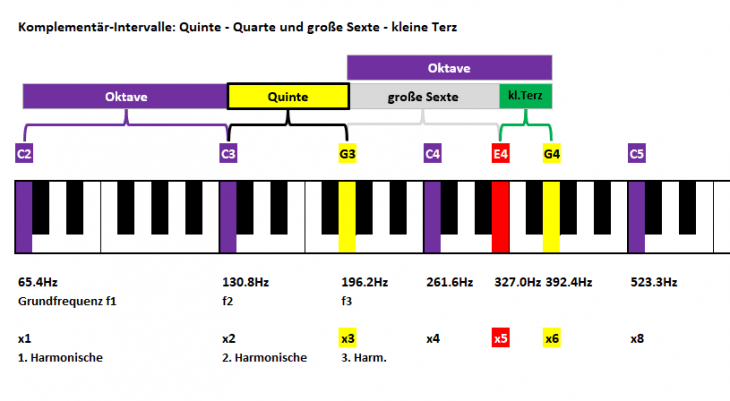
Deshalb gleich nochmal das Titelbild mit einer Klaviatur und einer sehr bewußt gewählten Anordnung der Intervalle und den Harmonischen 1 – 16 (hier basierend auf dem Grundton C2):

Wem hier sofort klar ist, auf was und mit welchen Facetten das Ganze hinauslaufen könnte, kann gleich mal ans Ende springen. Dort gibt es eine Zusammenfassung dieses Artikels und einen weiteren Appetithappen der zeigt, warum ich gerade diese Darstellung wähle.

[Kleine Anmerkung für die Angehörigen der „Saiten-Fraktion“: die Darstellung mit den Klaviertasten hat Vorteile bzgl. der Folge der Tonhöhen und ist gerade im weiteren Verlauf sehr hilfreich. Deshalb die Bitte an Euch, das erstmal einfach so auf Euch wirken zu lassen. Vielleicht inspiriert es zu einer entsprechend angepaßten Darstellung, die besser zu Gitarre, Geige & Co paßt. Für Rechtshänder und von oben gesehen ergeben sich bei der Gitarre die tiefsten Töne ja ebenfalls „mit der linken Hand ganz außen“, und höchste Töne „rechts kurz vor den pick-ups“. Allerdings hat z.B. die Gitarre 5 Saiten und damit liegen die Töne optisch nicht in einer Reihe.]

Für alle, die mehr Zeit mitbringen (können) – denn wir werden einen längeren Spaziergang durch die Oktaven machen – starten wir bewußt mit vertrauten Begriffen aus der Musik: Intervalle.

Quasi spielerisch am Instrument verknüpfen wir diese mit dem Begriff & Konzept der „Harmonischen“. Allerdings geht’s bei Letzteren nicht so sehr um Harmonielehre im engeren Sinn (das überlasse ich gerne denen die das draufhaben, und streife es eher nur ansatzweise).

Los geht’s!

Genug der Vorrede, starten wir mit etwas „Sound-Design“; hier per Excel-Engineering [zumindest was die Zeichnungen betrifft ;-)]. Experimentieren“ am eigenen Instrument schadet dabei nicht.

Pianisten, Keyboardern und Synthesizer-Freaks ist der Anblick unten sofort vertraut. Zudem ist auch die Piano-Roll Darstellung durch die weite Verbreitung von DAWs heute einem größeren Kreis jenseits der Tastenvirtuosen geläufig; allerdings muß man sich diese für das Leseformat erstmal zurechtlegen, d.h. um 90° in die Waagerechte kippen:

Ohne jegliches Vorwissen sehen wir zunächst eine Menge Tasten in weißer und schwarzer Farbe. Bei genauerem Hinschauen ergibt sich allerdings ein Muster sowie eine erkennbare Wiederholung (für Details das Bild bitte anklicken – oder einfach weiterlesen):

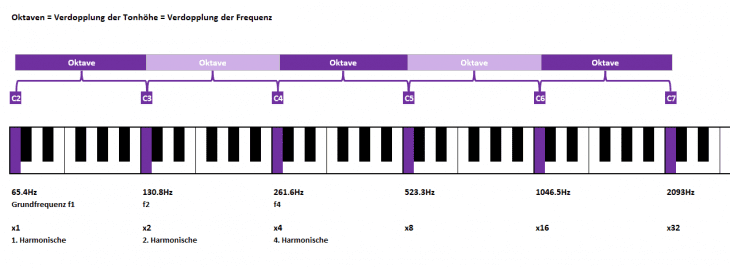
Damit ist bereits der erste wichtige Schritt zum grundlegenden Verständnis getan. Die Anordnung wiederholt sich also in regelmäßigem Abstand, und dabei verdoppelt sich die Tonhöhe mit jeder Wiederholung.

Das zugehörige Ton-Intervall heißt Oktave. So weit, so gut & allseits bekannt.

Hier das Ganze als Detailausschnitt für die Ansicht direkt im Text und die folgenden Schritte:

Es sind einerseits Notennamen (oberhalb der Klaviatur) und unten ihre physikalischen Pendants eingetragen (also Frequenzen in der Einheit Hz sowie zusätzlich mit dem Faktor x gegenüber der Frequenz des Grundtons, im Beispiel C2 mit Frequenz 65.4Hz und x1); andererseits Intervalle (ganz oben; hier Oktaven).

[Wichtiger Hinweis bzgl. Namensgebung der Notennummerierung und eine Erklärung gemäß Wikipedia zum „Kammerton“:

„Statt der Tonbezeichnung a1 (auch a‘ geschrieben, daher „eingestrichenes“ a) wird auch die internationale Bezeichnung A4 oder im MIDI-Protokoll A3 verwendet.“

Ich verwende hier ganz bewußt die internationale Bezeichnung, da diese mit der Zahl „4“ eine schöne Merkhilfe für den Kammerton A4 = 440Hz mitbringt. „International“ bedeutet heute typisch „Englischsprachig“ (sowie oft auch technisch), und als positive Eigenschaft verbinde ich das mit einem gewissen Pragmatismus. Das ist ähnlich wie mit den Bezeichnungen und Reihenfolge der Töne einer Tonleiter, die international ohne diesen Stolperstein A-H-C auskommt und stattdessen A-B-C verwendet ;-).]

Wir sehen durch die Verdopplung bei den Oktaven ein rasches Ansteigen des Faktors und somit der Frequenz; lassen uns dadurch trotz aktueller CV19-Situation nicht weiter verunsichern, nachdem Musikinstrumente schon seit Jahrhunderten diesem natürlichen Prinzip folgen und eine Infektion mit Musik eher angenehmer Art ist [OK; zumindest solange es dem eigenen Musikgeschmack entspricht ;-)].

Wenn wir diese Noten im Oktavabstand auf dem bevorzugten Instrument unserer Wahl spielen, werden wir bemerken, daß diese Töne immer gut zusammenpassen. Das erzeugt den Eindruck von Harmonie; und von daher kommt letztlich auch der Begriff „Harmonische“. Manches kann so einfach sein :-).

Das gilt zumindest bei allen natürlichen Instrumenten die tonalen Klänge erzeugen, d.h. solche deren Tonhöhe sich exakt entsprechend der gespielten Note verändern. Egal ob Flöte oder Trompete, Geige oder Gitarre, Klavier oder tonal spielbare Sounds am Synthesizer.

„Atonale“ Klänge wie z.B. Geräusche und Effektsounds des Synthesizers oder der Workstation zählen nicht dazu.

Woher kommt jetzt der Begriff „Harmonische“?

Dazu braucht‘s den einfachsten aller denkbaren Klänge, wie ihn eine Stimmgabel eine kurze Zeit nach dem Anschlagen erzeugt: einen reinen Ton bei einer einzigen Frequenz (z.B. A4 bei 440Hz). Klingt vielleicht a bisserl langweilig, kann im passenden musikalischen Kontext als Solo-Stimme mit entsprechender Tonfolge und virtuosem Spiel aber wirkungsvoller sein als so manche abgedroschene Dance-Trance-Super-Säge ;-).

Über der Zeit dargestellt und als elektrisches (!) Signal sieht das so aus und trägt den Namen Sinus: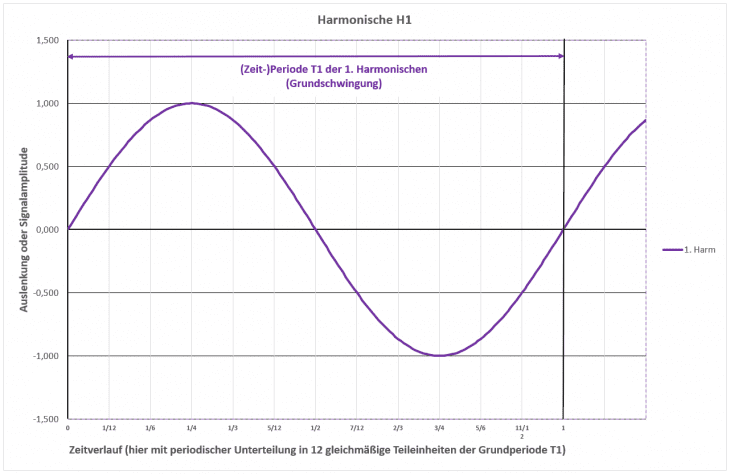

Die Dauer genau eines Durchlaufs (wie hier dargestellt) heißt Periode (Zeit in s, also Sekunden; meist deutlich kürzer), musikalisch von Bedeutung ist der rechnerische Kehrwert namens Frequenz (in der Einheit „Hertz“ Hz; Hörbereich ca. 25Hz … 16.000Hz je nach Alter oder/und Schädigung durch Überlastung).

Der Ausschlag nach oben und unten entscheidet dabei über die Laustärke und wird als Amplitude bezeichnet. Damit haben wir die wichtigsten Begriffe aus der Physik und belassen es damit für’s erste schon wieder; soll ja schließlich Spaß machen.

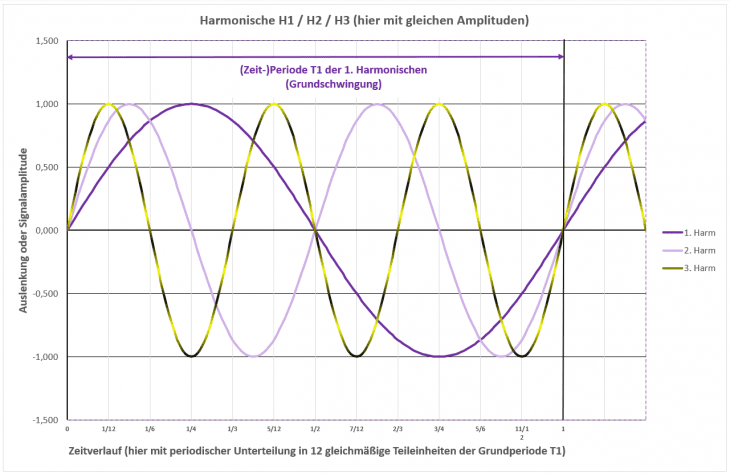
Praktischerweise und nicht ganz zufällig paßt ein Sinus-Ton mit der doppelten Frequenz genau zweimal in die gleiche Zeitperiode. Dieses Spiel läßt sich mit allen ganzen Zahlen 1/2/3/4/5… beliebig fortsetzen; hier als Beispiel für die Harmonischen 1 / 2 / 3:

Der Sinus-förmige Grundton wird dabei als 1. Harmonische bezeichnet. Sinus-Einzeltöne mit einem Vielfachen N dieser Grundfrequenz sind entsprechend die N-ten Harmonischen [Quak – Quak ;-)]. Diese bilden jedoch nicht immer ein musikalisches Intervall, wie wir im Verlauf noch sehen werden. Zur Farbgebung kommen wir gleich im weiteren Verlauf.

Ein französischer Mathematiker namens Fourier hat untersucht und bewiesen, daß sich tonale, periodische Klänge aus solchen einzelnen Harmonischen zusammensetzen (lassen). In einer späteren Folge werden wir uns das mal genauer ansehen.

Damit wieder zurück an die Klaviertastatur.

Bei genauem Hinsehen fällt sicher auf, daß mit der – heutzutage eher an Digitaltechnik erinnernden – Reihenfolge x1 / x2 / x4 / x8 / x16 / … einige Faktoren und somit Harmonische fehlen und es immer größer werdende Lücken gibt. Vor allem wollen wir nicht nur Töne im Oktavabstand spielen.

Die „reinen“ Intervalle: Oktave, Quinte und Quarte

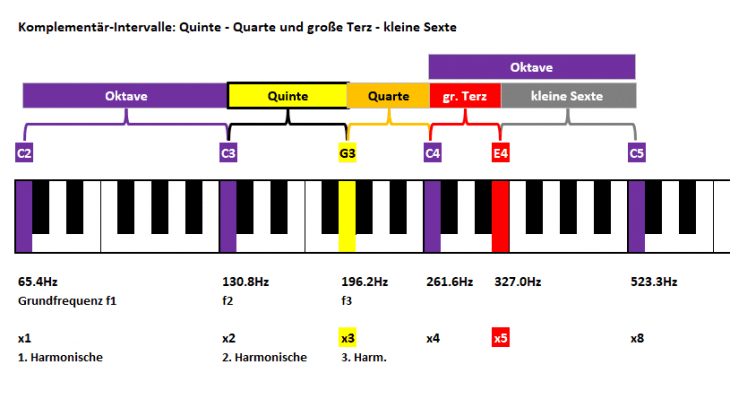
Schauen wir uns also an, wo wir die Harmonische Nummer x3 auf unserer Klaviatur finden können. „3“ sollte ja „irgendwo in der Mitte“ zwischen „2“ und „4“ liegen. Interessanterweise liegt diese (ausgehend vom Grundton C2) genau bei der Note G3 im Quint-Intervall zur 2. Harmonischen bei C3. Sie bildet zudem netterweise gleich noch eine Quarte mit der 4. Harmonischen bei C4:

Wir kümmern uns erstmal nicht groß um den Ursprung der Namen Oktave, Quinte & Quarte, aber erinnern uns schon mal an eine grundlegende Regel:

Musikalische Intervalle sind immer Frequenzverhältnisse, egal welcher tonale Klang dabei gespielt wird.

Im Fall einer Reihe von Sinus-Tönen mit Vielfachen der Frequenz des jeweiligen Grundtons spricht man von Harmonischen.

Für die ersten Intervalle gilt also:

• 2:1 := Oktave
• 3:2 := Quinte
• 4:3 := Quarte

Spielen wir C3 und G3 zusammen, fällt ebenfalls ein „harmonischer“ und „reiner“ Klang auf; allerdings hängt das hier bereits ein wenig von der gewählten Signalform des Oszillators ab (im Englischen typisch als „wave-form“ bezeichnet) ob man da schon eine gewisse „Bewegung“ wahrnimmt. Dasselbe gilt für G3 und C4.

Die ersten konsonanten Intervalle: große und kleine Terz

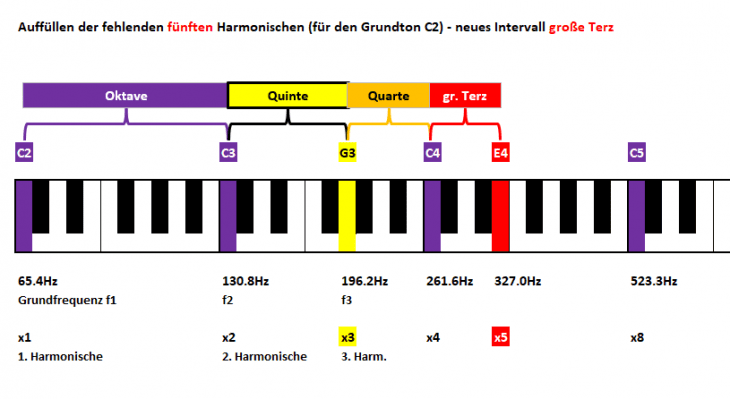
Wäre schön, wenn’s so simpel weitergehen würde., und tatsächlich gilt für No x5:

5:4 := große Terz

Die fünfte Harmonische liegt im Abstand einer großen Terz; hier also bei der Note E4:

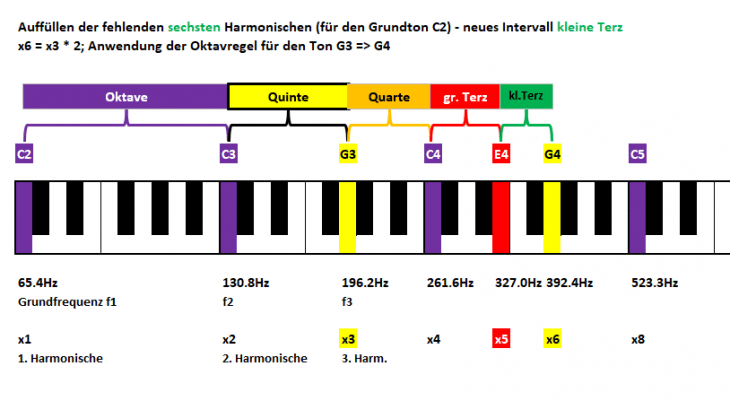
Wir freuen uns, und werden bei unserer Suche nach Nummer x6 schon beim Ton G4 fündig und somit einem weiteren einfachen Verhältnis:

6:5 := kleine Terz

Fassen wir es soweit zusammen:

• 2:1 := Oktave
• 3:2 := Quinte
• 4:3 := Quarte
• 5:4 := große Terz
• 6:5 := kleine Terz

Einfacher geht’s nun wirklich nicht, oder?

Wir konnten also in der Abfolge der Harmonischen x1 – x6 jedes Mal ein bekanntes Intervall zuordnen.

Das ist genau der Grund, warum ich hier diesen speziellen Blickwinkel bzgl. der Harmonischen wähle. Gerade die Intervalle, die wesentlich in (Grund-)Akkorden Verwendung finden, ergeben sich direkt aus der natürlichen Abfolge der Harmonischen!

Weiter stellen wir fest, daß sich ab hier eine zweite Reihe mit Frequenzverdopplung aufbaut: 6.te und 3.te Harmonische, also Verhältnis 2:1 und damit wieder eine Oktave.

Zudem gibt es eine weitere Quinte mit C4 und G4 – paßt zur Mathematik und klingt dabei auch noch schön :-).

Die ersten dissonanten Intervalle: große und kleine Sekunde

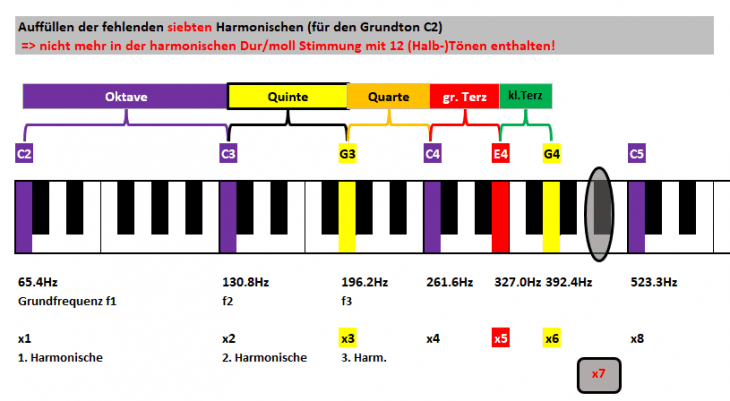
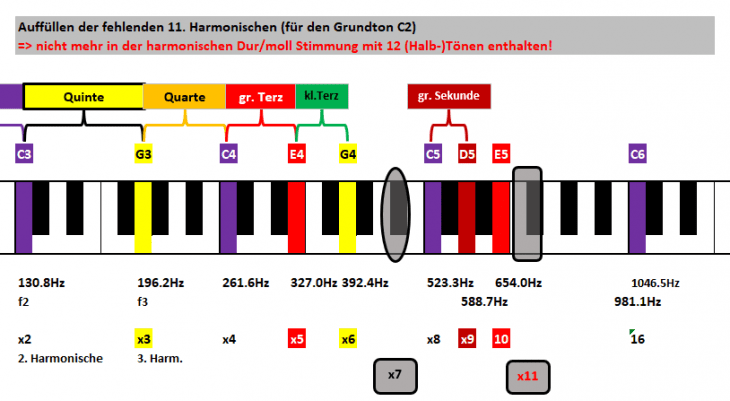
Jetzt wird‘s das erste Mal a bisserl interessanter. Wir kennen bereits die Lage von x6 (G4), und ebenso von x8 (C5). Die siebte Harmonische x7 muß also irgendwo dazwischen liegen, aber wo?

Die Frequenz ist dabei klar: 7x 65.4Hz = 457.8Hz.

An dieser Stelle gibt es aber einen ersten Bruch. Auf Instrumenten mit harmonischer Stimmung gibt es keine Note für die siebte Harmonische! Daher können wir im folgenden Bild nur den ungefähren Bereich angeben, in dem sich die 7.te Harmonische befindet – deshalb grau hinterlegt [wie „Graubereich“; als kleine Merkhilfe ;-)].

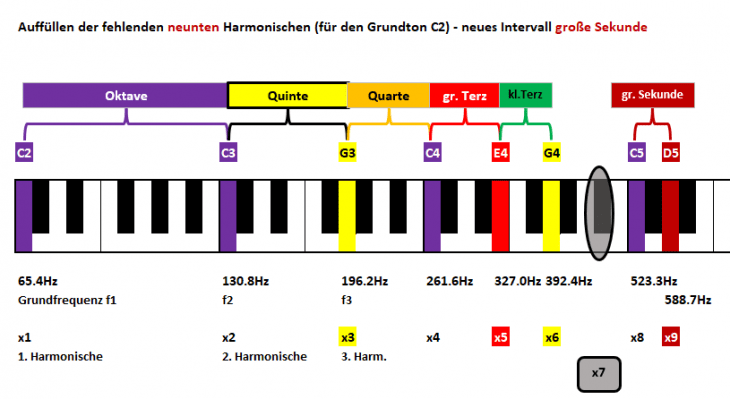
Da wir das erstmal nicht verstehen, laufen wir einfach weiter zur 9. Harmonischen. Diese ist fast direkter Nachbar zur 8.ten und liegt mit D5 einen Ganzton über C5; sprich einem Intervall von:

9:8:= große Sekunde

Im Verlauf der nächsten Harmonischen werden wir weiter so ein wechselndes Verhalten sehen.

Einerseits ergeben sich jetzt viele Harmonische bereits durch die Frequenzverdopplung von einer Oktave zur nächsten, hier für die 10. Harmonische und den Ton E5:

Andererseits finden wir mehr und mehr ungeradzahlige Harmonische, bei denen wir wieder keine entsprechenden Noten finden. Nächster Kandidat ist die Harmonische x11:

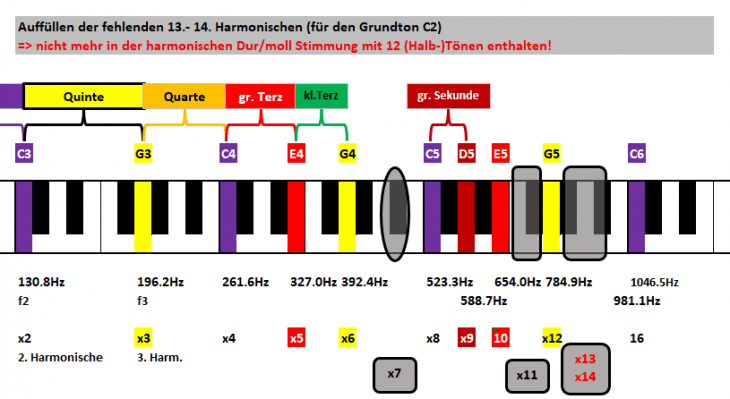
Nummer x12 ist wieder einfach; G4 nach G5:

Dagegen sind Nr. 13 und 14 wieder eigenwillig und liegen im Graubereich:

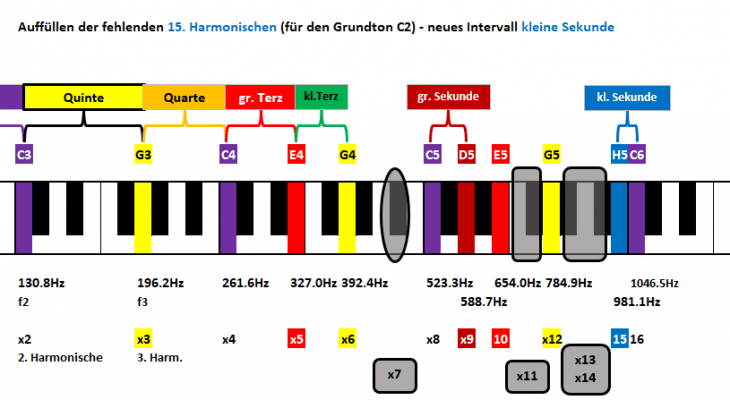
Erst mit der 15. Harmonischen treffen wir wieder auf eine Note: H5. Zunächst ergibt sich das aus der Quinte von E5 (x10). Gleichzeitig bildet sie aber ein bekanntes Intervall mit dem darauffolgenden C6 (x16):

16:15 := kleine Sekunde

Damit haben wir schon eine ganze Menge Intervalle; vor allem solche, mit denen sich die Tonleiter aufbauen läßt.

Allerdings haben wir noch nicht alle Töne, die für die C-Dur Tonleiter benötigt werden; es fehlen A und F.

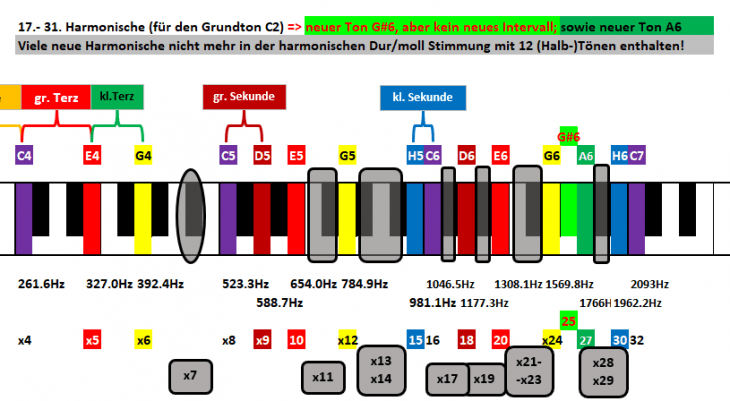
Also weiter geht’s von der 16.ten zur 32.ten Harmonischen und jetzt gleich als Zusammenfassung:

Mit der 25. Harmonischen auf G#6 kommt ein Ton dazu, der in der C-Dur Tonleiter überhaupt nicht auftritt. Er entsteht als große Terz zu x20 [25:20 = 5:4].

Nr. x27 ist das A6, auf das wir schon gewartet haben; hier als Quinte vo D6 (also 27:18 = 3:2). Damit fehlt für C-Dur nur noch das F.

Ansonsten liegen in diesem Bereich insgesamt 7 Harmonische, die keinen Tönen der harmonischen Dur/moll Stimmung entsprechen!

Vermutlich schwant dem einen oder anderen jetzt schon, was das später für den Mix bedeuten könnte; aber wir werden uns das in einer anderen Folge genauer ansehen.

Wir machen uns auf die Suche nach dem fehlenden F und marschieren von der 33.ten zur 64.ten Harmonischen – und da wird’s nochmal sehr interessant:

Zwar finden wir immer noch nicht unser vermißtes F [und dafür hebe ich mir das zur Farbskala passende kräftigere orange auf ;-)], dafür taucht überraschenderweise das Fis bei F#7 (x45) als Quinte (3:2) zum H6 (x30) auf. Somit neben dem G#6 ein weiterer Ton außerhalb C-Dur; und noch dazu mit einer sehr bemerkenswerten Eigenschaft: vom C7 zählen wir 6 Tasten bis zum F#7, und es sind ebenfalls wieder 6 Tasten bis zum nächsten C8 eine Oktave höher. Dieses Intervall hört auf den Namen Tritonus – im Bild hervorgehoben durch warmen Gold-Ton mit roter Umrandung – mit folgendem Frequenzverhältnis:

45:32:= Tritonus

Sieht eher nach einem etwas ungleichen Halbzeitstand beim Basketball aus, oder? ;-).

Das Ganze nochmal in voller Schönheit von 1 – 64 (besser auf das Bild klicken zwecks Vergrößerung):

Als Übersicht die Intervalle mit ihren Frequenzverhältnissen, wie wir sie bis jetzt identifiziert haben:

• 2:1 := Oktave
• 3:2 := Quinte
• 4:3 := Quarte
• 5:4 := große Terz
• 6:5 := kleine Terz
• 9:8 := große Sekunde
• 16:15 := kleine Sekunde
• 45:32 := Tritonus

Dabei fallen ein paar Dinge auf:

Von x1 bis x6 gibt es wie schon erwähnt durchgängig Intervalle der harmonischen Tonleitern; erst mit der 7. Harmonischen ergibt sich ein erster Bruch.

All diese Intervalle haben ein Verhältnis von benachbarten Harmonischen; mathematisch ausgedrückt (N+1) : N. Wir nutzen das – wenn überhaupt – nur als Merkhilfe.

Große Ausnahme ist der Tritonus mit 45:32.

Bis auf das „F“ haben wir so (am Beispiel des Grundtons C2) auch alle Töne der C-Dur Tonleiter gefunden, dazu noch G#6 und F#7.

In der Aufstellung fehlen noch die bekannten Intervalle große/kleine Sexte sowie große/kleine Septime – genau die suchen wir jetzt.

Die letzten fehlenden Intervalle: Sexte und Septime – jeweils groß & klein

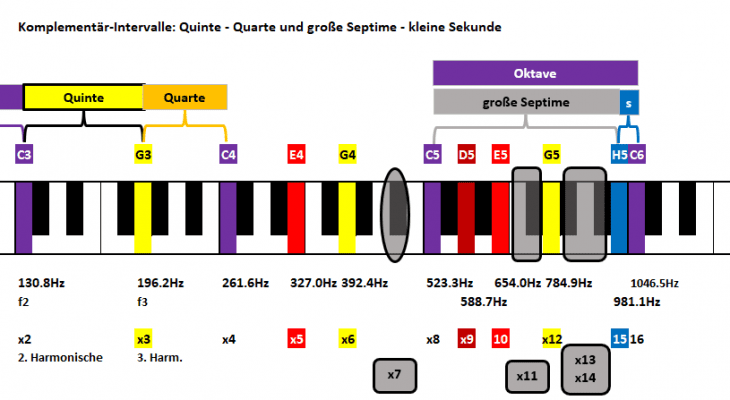
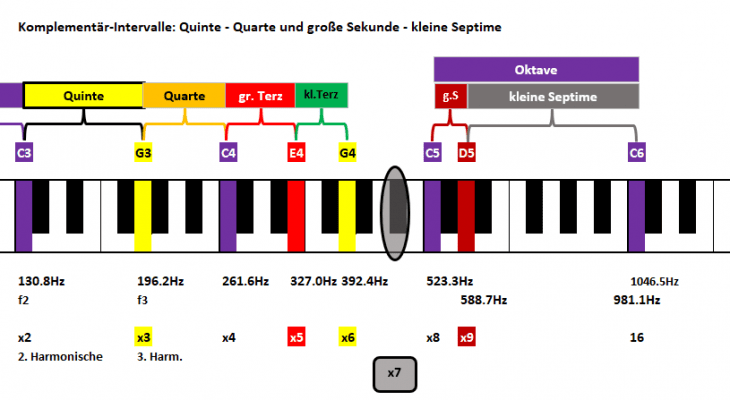
Für die Suche machen wir uns einer weiteren Systematik und Regelmäßigkeit zu Nutze: Komplementär-Intervalle.

Wir haben das bereits schon einmal gesehen: von C3 ging’s mit einer Quinte zu G3, gleich gefolgt von einer Quarte zu C4. Aufeinanderfolgende Quinte und Quarte ergeben somit eine Oktave.

Genau das gibt’s ebenso für die Terzen und Sekunden:

Terzen

• „Große Terz + kleine Sexte = Oktave“
• „Kleine Terz + große Sexte = Oktave“

Sekunden

• „Große Sekunde + kleine Septime = Oktave“
• „Kleine Sekunde + große Septime = Oktave“

Blicken wir also nochmal zurück und machen uns auf die Suche, ob und wo uns das vielleicht schon irgendwo begegnet ist. Also schön gemütlich Richtung „zurück auf Anfang“.

Nachdem wir eh schon beim mal C6 gelandet sind mit der kleinen Sekunde unmittelbar davor (H5), sollte die zugehörige große Septime so ja leicht zu finden sein. Sie erstreckt sich vom C5 (8. Harmonische) zum H5 (15. Harmonische); Frequenzverhältnisse:

15:8 := große Septime

Wir bleiben im Bereich C5 bis C6, da es von C5 auf D5 (9. Harmonische) die große Sekunde gibt. Damit geht die kleine Septime von D5 auf C6 (16. Harmonische) und kommt also im Breitwandformat 16:9 daher:

16:9 := kleine Septime

Nachdem das jetzt so schnell und einfach ging, sind wir trotz des langen Wegs durch die Oktaven gutgelaunt und vertrauen darauf, daß es für die fehlenden Sexten ebenso gilt. Innerhalb der Oktave vom C4 zum C5 gibt’s sowohl große und kleine Terz, da sollten also auch die Sexten in der Nähe sein.

Von C4 auf E4 hatten wir die große Terz, mit E4 als 5.te Harmonische. Mit der Oktavregel für Komplementär-Intervalle finden wir die nächste Oktave bei C5 und der 8. Harmonischen. Somit gilt für die kleine Sexte:

8:5 := kleine Sexte

Fehlt nur noch die große Sexte; die hat sich zwar a bisserl versteckt, zeigt sich mit unserem aufgefrischten Wissen aber bei genauem Hinschauen. Von E4 (5. Harmonische) auf G4 gibt’s eine kleine Terz, die wir zur Suche der großen Sexte brauchen. Gehen wir von E4 aber zurück auf G3 (Oktavregel!), finden wir genau die große Sexte; Frequenzverhältnisse also:

5:3 := große Sexte

Im Bild ist diesmal bewußt die resultierende Oktave mit eingezeichnet, da sich diese hier über einen „neuen Grundton“ G3 (also die 3. Harmonische vom Grundton C2) zum G4 (6. Harmonische) erstreckt. 6:3 = 2:1 := Oktave.

So nebenbei sehen wir damit, daß dieselben Gesetzmäßigkeiten offenbar ebenso für andere Grundtöne gelten. Das ist auch gut so und bildet die Grundlage für jede Art harmonischer Musik. Wir erinnern uns weiter, G3 bildet zudem eine Quinte mit C2. Wer jetzt an den Quintenzirkel denkt, liegt genau richtig.

Zurück zu den Intervallen und zur Übersicht alle Frequenzverhältnisse für Sexten und Septimen:

Konsonant

• 5:3 := große Sexte
• 8:5 := kleine Sexte

Dissonant

• 15:8 := große Septime
• 16:9 := kleine Septime

Wir stellen fest, daß wieder nur die Harmonischen beteiligt sind, die wir von den anderen Intervallen schon kannten.

Viele andere ungeradzahlige Harmonische treten nicht in den Intervallen der harmonischen Stimmung auf.

Dem ein oder anderen fällt vielleicht auf, daß ich zwar Attribute wie „rein“, „konsonant“ und „dissonant“ aufgeführt, allerdings nicht weiter erläutert habe. Einerseits kennen viele unter uns die Hintergründe für diese Beschreibung. Andererseits ist gerade ein Durchgang durch verschiedene Signalformen eine gute Möglichkeit, gewisse Facetten zu beleuchten.

Gesamtübersicht und Zusammenfassung über die Intervalle

Die bekannten Intervalle wurden hier anhand ihres „ersten“ Auftretens in den einzelnen Oktaven einer „harmonischen“ Frequenzabfolge als Vielfache der Frequenz eines Grundtons hergeleitet.

Zur (indirekten) Darstellung der Frequenzen wird die – Musikern bestens vertraute – Klaviatur an Stelle einer technischen Frequenzskala verwendet, um so den direkten Bezug zu Noten und ihren dazugehörigen Frequenzen zu schaffen.

Musikalische Intervalle sind immer Frequenzverhältnisse, egal welcher tonale (!) Klang dabei gespielt wird.

Im Fall einer Reihe von Sinus-Tönen mit Vielfachen der Frequenz des jeweiligen Grundtons spricht man von Harmonischen (die aber nicht immer ein musikalisches Intervall bilden).

Für die Abfolge der Harmonischen x1 – x6 gibt es immer ein musikalisches Intervall (gemäß der harmonischen Stimmung); und sie treten innerhalb eines Umfangs von 2 Oktaven und einer Quinte auf.

Die sehr kleinen Intervalle große und kleine Sekunde treten in der natürlichen Abfolge der Harmonischen dagegen erst in der 4. Oktave auf. Das ist in gewisser Weise bemerkenswert, da gerade sie ja die Einzel-Tonabstände in der harmonischen Tonleiter bestimmen.

Reine Intervalle

• 2:1 := Oktave
• 3:2 := Quinte
• 4:3 := Quarte

Konsonante Intervalle

• 5:4 := große Terz
• 6:5 := kleine Terz
• 5:3 := große Sexte
• 8:5 := kleine Sexte

Dissonante Intervalle

• 9:8 := große Sekunde
• 15:8 := große Septime
• 16:9 := kleine Septime
• 16:15 := kleine Sekunde

In sehr hohen Oktavlagen liegen die Harmonischen auf fast allen Tönen der jeweiligen Tonleiter (im Beispiel C-Dur auf dem Grundton C2); und es gibt ebenso viele Harmonische die nicht mehr zu Tönen der harmonischen Dur-/moll-Tonleiter passen.

Wer sich tapfer bis hier durchgearbeitet hat und sich das Ganze sowie die vielen Bilder mal im Schnelldurchlauf quasi als „YouTube-light“ anschauen möchte, kann sich diese einfach runterladen. Die Nummerierung und die Namen der Dateien sind bewußt in der gleichen Reihenfolge wie bei unserem Rundgang.

Im Sinne eines „open source“ Gedankens der link zu einer ZIP-Datei mit den ganzen Bildern [korrigierte Versionen wie jetzt auch im Text; vielen Dank an die Hinweise aus dem Leserkreis :-) !]; sowie der sehr einfach gestrickten Excel-Datei <<Harmonische_Intervalle_2021-03-16.xlsx>> (Excel im Office 2019 Format) mit den Rohdaten; es sind keine Macros enthalten:

Intervalle_Harmonische_2021-03-17

Vielleicht regt dieser Artikel und die Art der Darstellung den einen oder anderen mit Programmierkenntnissen ja zu Erweiterungen an, sich die Harmonischen auch für andere Noten als „C“ ausgeben zu lassen.

Wie eingangs angesprochen wäre es auch interessant, ob es eine Form gibt, die für andere Saiteninstrumente „griffiger“ ist.

Ausblick

Bisher gab’s für die meisten sicher kaum wirklich Neues, vielleicht mit Ausnahme der – sehr langen – schrittweisen und farbenfrohen Ableitung der Intervalle und Darstellung auf der Klaviatur gemäß der natürlichen harmonischen Abfolge durch Frequenzvervielfachung.

Beim nächsten Mal ergänzen wir das Ganze dann um einen weiteren wichtigen Aspekt: den Lautstärken der einzelnen Teiltöne; oder eben den Amplituden der Harmonischen. Ja, und wo kommen die Harmonischen eigentlich her?

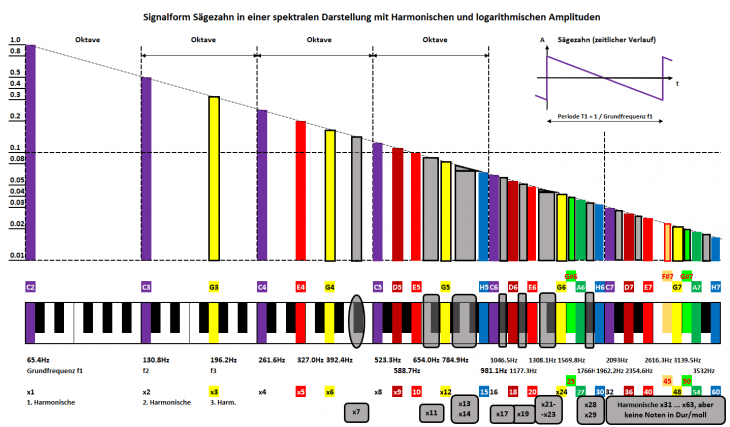
Als Appetitanreger schon mal eine kleine Vorschau über die Amplitudenverhältnisse (hier gleich im eleganten logarithmischen Maßstab) für den beliebten Sägezahn (wieder auf dem Grundton C2), den es nicht nur bei Synthesizern zu finden gibt. Das Ganze wieder sehr Musiker-freundlich präsentiert mit einer Klaviatur und Noten als Frequenzachse, damit es eine direkte – bei Klavier & Keyboard im wahrsten Sinne des Wortes sicht- und (be)greifbare –Verbindung zum Instrument ergibt.

… und wer sich bis jetzt gefragt hat, warum ich denn die einzelnen Intervalle immer nur Stückchen für Stückchen während des langen Spaziergangs durch die Oktaven abgeleitet habe und Töne mit Farben hinterlegt habe, dem geht hier vielleicht ein Licht auf (und für Details wie gewohnt bitte zum Vergrößern auf das Bild klicken):

So, ich denke nach diesem fast schon psychedelischen Farbrausch müssen sich die Augen erstmal wieder erholen ;-) – andererseits ist ein Regenbogen draußen ja auch immer wieder schön anzuschauen :-).

Hinweise zu weiterführenden Betrachtungen:

Buchtipp

„Die neue Harmonielehre“ von Frank Haunschild; AMA-Verlag; ISBN 978-3-927190-00-9

Links

Wikipedia

http://„Kammerton“: https://de.wikipedia.org/wiki/Intervall_(Musik)

http://“Intervall (Musik)”: https://de.wikipedia.org/wiki/Intervall_(Musik)

AMAZONA: Workshop zu Harmonielehre

https://www.amazona.de/harmonielehre-verstehen-anwenden-01-dur-moll/

https://www.amazona.de/harmonielehre-verstehen-anwenden-02-intervalle/

https://www.amazona.de/harmonielehre-verstehen-anwenden-03-akkorde-terzen/