Waveshaping in der Theorie
Knarz! Schmatz! Bfräuioääum!
Waveshaping ist die Erweiterung von Overdrive. Damit lässt sich ein Klang mit wenigen Parametern subtil bis extrem verfremden. Ultra-derbe, dreckige Verzerrungen, aber auch weich fließende komplexe Klangverläufe ermöglicht diese Synthese. Im „Winzig-Welle 2/XT/XTk/PC“ enthält der Waveshaper Filter den flexibelsten Shaper. Damit verwandt ist der Sin>LP-Filter. Auch der Mixer vor dem Filter kann das Audio-Signal auf 2 mögliche Arten verzerren. Darüber hinaus verfügt der MW2 über einen Overdrive als Effekt.
Letztendlich kann man zwar nur durch Ausprobieren, Ausprobieren und nochmals Ausprobieren Sounds zusammenschrauben. Es gibt aber Fälle, wo winzige Änderungen an einem Parameter den Klang radikal verdrehen können. Beim Waveshaper Filter im XT ist das der Fall. Es kann dann doch sehr hilfreich sein, das Verhalten eines Waveshapers zu verstehen, wenn man gezielt eine bestimmte Art von Klang hinzubekommen versucht. Deshalb beginne ich mit den Grundlagen der Waveshaping-Synthese und erkläre, was die Shaper im MW2 mit den Wellen so anstellen.
Bitte nicht gleich erschrecken und weg klicken!!! Die Mathematik bleibt garantiert auf total simplem Schul-Niveau.
1) Was ist Wave-Shaping?
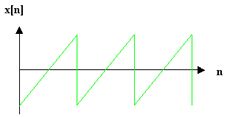
Ein Shaper ist eine Funktion f(x), die nur von einer (zeitabhängigen) Variablen x[n] abhängt. x[n] ist das n-te Sample eines Event- (Steuer-) oder Audio-Signals. n ist also gleichbedeutend mit der Zeit, die ja in digitalen Systemen mit der Sampling-Rate quantisiert ist.
Alternativ kann man sich einen Shaper auch als Tabelle vorstellen, welche jedem Input-Wert x einen Output-Wert y = f(x) zuordnet.
Trivialer Spezialfall: Die lineare* Funktion f(x) = a * x mit Konstante a ist ein Verstärker. Sie macht ein Audio-Signal einfach nur leiser/lauter, ohne den Klang zu beeinflussen. Die Bezeichnung „Shaper“ verdienen nur die nicht-linearen Fkt.en.
*linear: Eine Funktion ist genau dann linear, wenn gilt:
- f(a*x) = a * f(x),a = const
- f(x + y) = f(x) + f(y)
Beide Gleichungen kann man auch zusammenfassen: f(a*x + b*y) = a*f(x) + b*f(y), a,b = const
Nicht-lineare Funktionen bewirken bei Audio-Signalen eine Verzerrung der Welle, welche das Spektrum auf ganz wilde und sehr schwer zu bes chreibend verändert. Die einen Obertöne können dabei verstärkt oder hinzugefügt, andere gleichzeitig abgeschwächt werden, wie ein sehr komplexer Filter. Kann man etwa sagen, ein Shaper sei ein Filter? Nö.
Unterschiede: Filter <-> Waveshaper:
Filter: Reagiert nur auf das Spektrum. Die Form der Input-Welle ist ihm völlig schnuppe. Die Phasen der Harmonischen können beliebig verschoben sein (was die Wellenform, aber nicht den Klang verändert). Er verändert das Spektrum gezielt (Nebeneffekt: Wellenform ändert sich natürlich).
Außerdem ist er linear*. Das bedeutet:
- Ändert sich die Amplitude des Eingangs um Faktor a, dann auch nur die Amplitude des Ausgangs um Faktor a. Das Specktrum bleibt aber unverändert.
- Es ist egal, ob 2 Wellen zuerst addiert oder gefiltert werden. Man hört keinen Unterschied, ob der Sound aus 1 Stimme besteht, in der 2 verstimmte
Sägezähne mit gleicher Amplitude gefiltert werden, oder ob es sich um 2 verstimmte Stimmen handelt, in denen jeweils nur ein Sägezahn schwingt.
Waveshaper: Reagiert nur auf die Wellen-Form. Das Spektrum der Input-Welle spielt keine direkte Rolle. Die Phasen der Harmonischen können deshalb NICHT beliebig verschoben sein, denn das würde ja die Wellenform verbiegen. Er verzerrt die Wellenform gezielt. Das hat fast immer den Nebeneffekt, dass sich das Spektrum auf komplexe Weise ändert.
I.a. ist die Shaper-Funktion nicht-linear:
- Ändert sich die Amplitude des Eingangs, dann meistens auch die Wellenform und damit das Spektrum.(Ausnahmen: z.B. f(x) = x²; f(a * x) = a² * x² Die Welle x² ändert sich nur in der Amplitude, die Form und damit das Spektrum bleiben konstant; das gilt generell für Potenz-Fkt.en).
- Es ist ein großer Unterschied, ob 2 Wellen zuerst addiert oder verzerrt werden. Verzerrt man die Summe zweier gleicher, verstimmter Oszillatoren, dann hört man eine periodische, wabernde Klang-Veränderung, die je nach Shaper-Funktion mehr oder weniger dreckig und seltsam klingen kann.
Will man eine normale Detune-Schwebung hören (wie ohne Verzerrung), dann muss man im MW2 2 verstimmte Stimmen pro Note einsetzen und pro Stimme nur einen Oszillator shapen (oder beide, aber nicht verstimmt).
Während FM eine Welle horizontal (zeitlich) verzerrt, verbiegt Waveshaping sie vertikal.
Wenn ein Shaper direkt nach einem Oszillator geschaltet ist, dann entsteht eine neue konstante Wellenform, ein neues harmonisches Spektrum, das beliebig gefiltert werden kann.
Noch viel faszinierender ist Shaping HINTER einem Filter. Am bekanntesten ist Filter-Overdrive, der einen dumpfen Tiefpaß-gefilterten Klang wieder mit neuen, aber anderen Harmonischen anreichert und ihn so von warm und grungy bis knarzend rau macht. Diese Post-Filter-Distortion macht die Arbeit des LP-Filters, für die er eigentlich gedacht war (obere Harmonische dämpfen), wieder zunichte. Der Filter wird vielmehr dazu zweck-entfremdet, die Wellenform des Oszillators zu verändern. Obwohl sich ein Filtersweep ganz weich anhört und das Spektrum sich dabei langsam morpht, verändert der Filter die Wellenform des Filter-Ausgangs sehr drastisch, selbst bei langsamer Eck-Frequenz-Modulation und vor allem bei hoher Resonanz. Und der Shaper reagiert ja direkt auf Wellenform-Änderungen,
so dass der Shaper-Ausgang wahnsinnig schnell morpht. Ergebnis: wilder, verrückter, drastischer Klang-Verlauf.
Einen Haken hat die Sache hat allerdings doch: Aliasing. Auch wenn der Oszillator Band-begrenzt (Aliasing-frei) ist, fügt der Shaper dem Spektrum meistens auch Frequenzen hinzu, die oberhalb der halben Sampling-Rate liegen. Ein digitales Audio-System kann solche Obertöne nicht richtig wiedergeben, sondern spiegelt deren Frequenz an der halben Sampling-Rate und produziert dissonante falsche Töne, die metallisch vibrieren. Muß aber nicht unbedingt grässlich klingen, vor allem aggressiven Verzerrer-Sounds verleiht das zusätzliche digitale Würze.
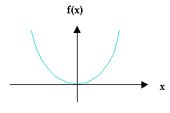
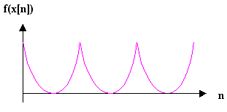
Bspl: a) Parabolische Verzerrung: f(x) = x²
Alle Eingangs-Samples werden quadriert. Eine Sägezahnwelle z.B. wird zu einer (Oberton-ärmeren) Parabol-Welle verzerrt. (Dazu braucht man eigentlich keinen Shaper; es geht auch mit Ring-Modulation: 2 gleichphasige Sägezähne multiplizieren.)
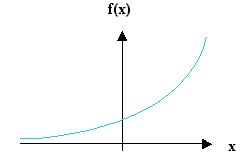
b) Exponentiator: f(x) = a*exp(b*x) mit Konstanten a, b.
Wird häufig für Steuer-Signale eingesetzt. Damit rechnet ein Synthesizer die Tonhöhe in die Frequenz um, mit der er einen Oszillator laufen lässt. Und überhaupt alle logarithmisch skalierte Parameter wie Lautstärke, LFO-Rate und Hüllkurven-Zeiten werden so umgerechnet.
c) Hard-Clipping: f(x) = {x , falls |x| <= 1
{-1 , x < -1
{+1 , x > +1
Das Signal x wird abrupt begrenzt auf den Wertebereich [-1;+1]. Dumpfe Wellen werden mit vielen Harmonischen angereichert. Bei Verwendung als Filter-Overdrive ist das Klangergebnis ist rau kratzend, gut für harte Sounds.
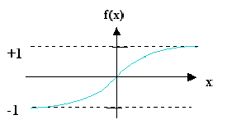
d) Soft-Clipping / Sättigung: z.B. f(x) = (arctan x)/Pi
oder f(x) = sign x * (1 0.25 / (|x| + 0.25)) (aus Hyperbeln zusammen gesetzt)
oder f(x) = 1 (x – 1)² , falls 0 <= x < 1
{-1 + (x + 1)², -1 < x < 0
{1 , x >= 1
{-1 . x <= -1 (aus Parabeln Knick-frei zusammen geschustert)
Das Signal x wird weich begrenzt auf den Wertebereich [-1;+1]. Im Gegensatz zum Hard-Clipping wird das Signal nicht abrupt abgeschnitten, sondern geht allmählich in die Sättigung über. Das fügt dumpfen Klängen eher tiefe und mittige statt hohe Harmonische hinzu. Es gibt viele mögliche Kurven, die das bewerkstelligen, sie unterscheiden sich aber im Klang.
Analoge Tonbänder haben eine solche Sättigungs-Kennlinie, die dem Mix eine warme Charakteristik verleiht. Aus diesem Grund ziehen viele Produzenten immer noch analoge Bandmaschinen digitalen Recording-Systemen vor.
Sehr gut geeignet auch für Filter-Overdrive. Schwache Verstärkung vor dem Sättiger resultiert in warmem, sanftem Grunge. Bei extrem hoher Vor-Verstärkung knarzt es genau so scharf wie Hard-Clipping.
2) Mixer-Clipping: Overflow und Saturation
Ist im Handbuch auf Seite 46 beschrieben.
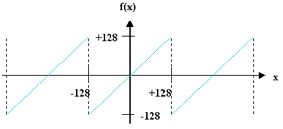
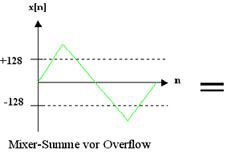
Overflow Verzerrung: Auf Samples der Mixer-Summe (Ringmod + Rauschen + Wave1 + Wave2), welche im verbotenen Bereich >128 oder <-128 sind, wird
256 bzw. +256 dazu addiert, so dass alle Output-Samples letztendlich im erlaubten Bereich [-128;128] sind. Das simuliert den numerischen Überlauf im Microwave 1.
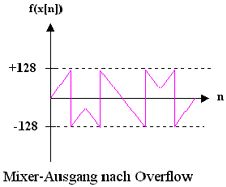
Die scharfen Sprungstellen, die beim Overflow-Clipping entstehen, sind äquivalent zum Hinzufügen von Rechteckwellen (mit variabler Puls-Breite). Man kann sich das Overflowing auch so vorstellen, dass, falls der Pegel der Mixer-Summe zu hoch ist, magische Pulswellen dazu gemischt werden (Graphik). Diese Pulse kann man auch gezielt in der Pulweite modulieren, indem man die Amplituden der Mixer-Eingangs-Quellen moduliert.
Overflow: f(x) = {x , falls |x| <= 128
{x-256 , +128 < x <= 384
{x+256, -384 <= x < -128
(Diese Formel reicht aus, wenn man nur Wave1+2 und Ringmod im Mixer aufdreht. Die Summe überschreitet dann nie 3*128=384. Mischt man aber auch noch Noise oder den externen Eingang dazu, kann ein Summen-Sample durchaus 2-mal überlaufen.)
Man bedenke aber, dass mit Overflow starkes Aliasing einhergeht.
3) Sin(x)->LP-Filter
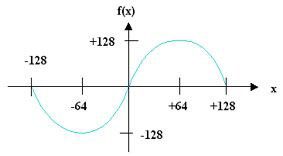
Hier ist ein Sinus-Shaper nach dem Mixer und VOR einem 12dB-LP-Filter geschaltet. Weil der Mixer-Output immer auf [-128;+128] begrenzt ist, reicht die Defininitons-Menge [-128;+128] aus. Bei steigender Amplitude des Input-Signals wird dieses zuerst oben und unten weich zusammen gedrückt. Überschreitet die Amplitude 64, werden Täler und Berge nach innen verbogen.
Sinus-Shaper: f(x) = 128 * sin (p /128 * x), -128 <= x <= +128
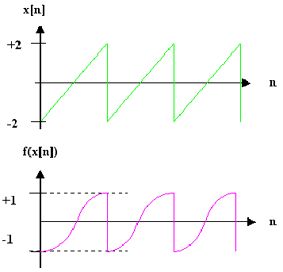
Bsple: 2 Waves mit steigender Amplitude werden immer stärker zerquetscht.
Kombiniert man Sin>LP-Filter mit Overflow Mixer Clipping, dann werden die Overflow-Sprungstellen sogar total eliminiert, weil die Signal-Werte 128 und +128 zu 0 hingebogen werden. Die resultierende Verzerrung kann sogar weicher klingen als mit Saturation Mixer Clipping.
4) Waveshaper Filter
Erstens ist im Gegensatz zum Sin(x)->LP-Filter der Shaper NACH einem 12dB-LP-Filter geroutet. Das ermöglicht grungy Filter-Overdrive und noch durchgeknalltere Sachen. Zweitens kann man als Shaping Kurve eine beliebige Wave aus der aktuellen Wavetable auswählen (Shaper-Wave). Genau das macht den Shaper zu einem hyper-flexiblem Verzerrer, der weitaus mehr kann als nur gewöhnlichen Hard/Soft-Overdrive, der in vielen anderen analogen/virtuell-analogen Synthesizern verbreitet ist.
Schnelle Filter-Sweeps bei hoher Resonanz erzeugen damit harte, wahnsinnige, dreckige bis kreischende Verzerrungen. (Grund: Siehe Kapitel 1)
Weiche Klang-Verläufe erhält man mit sehr, sehr langsamen Filter-Sweeps und tiefem Cutoff, oder ganz ohne Filter, indem man nur die Amplitude eines oder beider Oszillatoren im Mixer langsam moduliert.
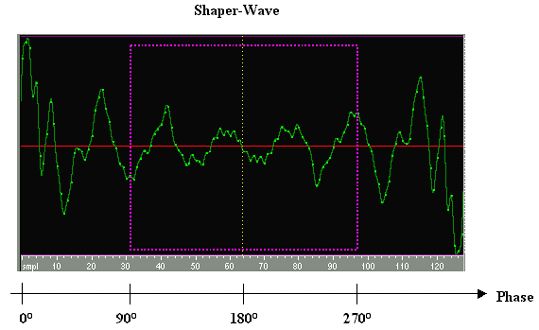
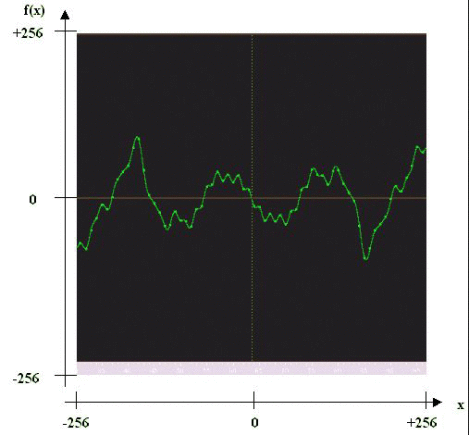
Wie sieht die Verzerrungs-Kurve f(x) genau aus, die aus einer bestimmten Shaper-Wave generiert wird? Kurz gesagt: Wie die Shaper-Wave von 90° bis 270° (Samples 32 … 97), aber linear interpoliert.
Genauer:
Die Filter-Output-Amplitude ist auf 256 begrenzt (das Doppelte des Mixer-Outputs), egal wie hoch die Resonanz ist. Also muss die Definitions-Menge der Shaper-Funktion [-256;+256] sein. Die Werte-Menge ist dann sinnvollerweise auch [-256;+256].
Ein Wave-Zyklus hat immer 128 Samples. Meistens hat die Wave eine ungerade Symmetrie: die 2. Hälfte ist ein Spiegelbild der 1. Hälfte und wird durch Punkt-Spiegelung am Punkt (64,5 ; 0) generiert. Formal:
Wave[65 + n] = -Wave[64 – n], n = 0, …, 63
Von den ROM-Wavetables im Microwave 2 ist WT 65 „True PWM“ (welches den normalen Puls-Oszillator emuliert) das einzige, das NICHT diese Punkt-Symmetrie besitzt.
Relevant sind nur die letzten Samples 32 bis 97 der Shaper-Wave; die ersten und letzten 31 sind völlig wirkungslos. Zwischen benachbarten Shaper-Samples wird linear interpoliert, die Kurve ist daher ein stetiger Polygon-Zug; Sprungstellen kann es deshalb keine geben, sondern nur steile Flanken.
Der Definitions-Bereich [-256;+256] entspricht dem Sample-Bereich [32,5 ; 96,5]. Input -256 wird abgebildet auf dem Mittelwert der Samples 32/33:
f(-256) = (Wave[32] + Wave[33]) / 2; f(+256) = (Wave[96] + Wave[97]) / 2;
Der Funktions-Graph gleicht dem Wellen-Zyklus von 90° bis 270° (Samples 32 … 97), aber mit dem Unterschied, dass benachbarte Samples durch gerade Linien verbunden werden anstatt einer runden Interpolation. Im Bild „Shaper Wave“ markiert die rosa Linie eben diesen Graphen.
Shaper-Funktion f(x)
Und jetzt shapen wir mal mit dieser Funktion eine Dreiecks-Welle mit zunehmender Amplitude (ohne zu filtern):