Das Geheimnis digitaler Filter
Immer wieder wird der Versuch unternommen, das Klangverhalten analoger Filter digital zu emulieren. „Wie erzeugt man digitale Filter die analog klingen“ war auch die Frage die sich Dave Rossum einst stellte und darüber einen Aufsatz schrieb, der Geschichte machte. Die deutschsprachige Übersetzung lieferte nun für AMAZONA.de TobyFB:
Es gibt Artikel-Anfragen im Leben eines AMAZONA.de-Autors, da überlegt man nicht lange und sagt einfach: „Ja“.
Während Peter Grandl über Wochen Dave Rossum, einst Gründer und Chef-Entwickler von E-Mu, interviewte, widmete ich mich der Übersetzung seines Aufsatzes „Making Digital Filters Sound Analog“, den Dave bereits 1992 verfasste, kurz nachdem er mit dem H-Chip das erste digitale Filter in einem Sampler verbaute (E-Mu EMAX II), der einen überzeugend analogen Klangcharakter hatte.
Parallel empfehlen wir daher auch die Lektüre des vierteiligen Interviews mit Dave Rossum:
Auch wenn der Artikel schon einige Jahre auf dem Buckel hat, Staub angesetzt hat er noch nicht. Im Gegenteil, Dave Rossums Forschungs- und Entwicklungsarbeiten sind nach wie vor hoch aktuell. Vor allem als Ergänzung zum mehrteiligen Interview mit Dave Rossum, ist dieser Aufsatz ein wertvolles Dokument über einen Visonär, der ohne Übertreibung mit Steve Jobs oder Bob Moog in einem Atemzug genannt werden sollte.
Für die AMAZONA.de Gemeinde habe ich nun mein leicht verstaubtes Englisch aus der Kiste gekramt. Bitte seht mir also ein paar Übersetzungsschwächen nach, auch ist es nicht immer einfach, Rossums teils sehr „nerdigen“ Humor mit ins Deutsche zu übertragen. Das englische Original findet ihr als PDF zum Donwload in der Linkliste.
Vor einigen Wochen haben wir übrigens das selbe Thema bereits einmal ähnlich, aber allgemein leichter verständlich beleuchtet: BITTE HIER KLICKEN.
Legen wir los:
Wie bekommen Digitale Filter einen „analogen“ Klang?
von Dave Rossum / E-Mu-Systems 1992
- Einführung, abstrakt
Frühere elektronische Synthesizer besitzen einen charakteristisch-„analogen” Klang, weitgehend erzeugt durch typische Verzerrungen ihrer spannungskontrollierten Filter. Rechnerbasierende Musiksynthese-Techniken arbeiten häufig mit der Speicher- Sättigungsmethode des zyklischen Überlaufschutzes zur Laufzeit. Die Veränderung von Filterparametern führt hier zu einem harten, unnatürlichen Klang während der Filterüberlastung (Übersteuerung, Überlauf). Während einzelne Simulationen oder physikalische Modelierungstechniken das nichtlineare Verhalten von einzelnen analogen Filtern mit willkürlicher Genauigkeit und Beschränkungen der Rechentiefe umsetzen, verhindern eben diese Beschränkungen eigentlich den musikalischen Einsatz außerhalb des wissenschaftlichen Interesses.
Wie dem auch sei, einige sehr einfache Veränderungen zu bekannten digitalen Filtern bieten bemerkenswertes „analoges“ Verhalten mit einem gering erhöhten Rechenaufwand. Dieses Dokument stellt einige der Modifikationen dar und erläutert die Gründe hinter den Einflüssen auf die Überlastungs- und die Verzerrungscharakteristik der Audio-Signalausgabe. Einige hier dargebotene Hörbeispiele illustrieren verschiedene Verhalten, „Soft Limiting“ und die zeitliche Veränderung der Filterresonanz sowie die Rückkehr zum Anfangswert der Resonanz. (Anmerkung des Verfassers: Da uns die Originalbeispiele nicht zur Verfügung standen, wurden diese von Peter Grandl beigesteuert.) Ihr findet sie hier:
- Einführung
Der Prozess dynamischer Klangfilterung zur Ausdrucksherstellung bei Noten war die Basis der modernen Musiksynthesizer. Der berühmte „Moog-Klang“ und der vieler anderer elektronischer Instrumente basierten auf der subtraktiven Synthese wie beispielsweise in einem spannungskontrollierten analogen Tiefpass-Filter. Musiker beklagen heute oft den Verlust dieses warmen und ausdrucksstarken Timbres in der Gegenwartsmusik. Es ist sicher wahr, dass das Design eines vergleichbaren, digitalen Filter für Tonsignale viele Studenten der digitalen Signalverarbeitung vor ein Problem stellt, für das sie nicht mit Wissen ausgestattet wurden.
Somit ist die Lösung des Problems, (wie bekommen digitale Filter einen „analogen“ Klang), die Simulation eines analogen Filters. Die Herstellung dieses Filters ist auf musikalischer Ebene sowohl eine erstklassige Ingenieursleistung als auch musikalisch ein exzellentes Ziel.
- „Small Signal Behavior“ – Kleinsignalverhalten
Das Hauptproblem beim Kleinsignalverhalten digitaler Filter wird als Quantisierungsrauschen betrachtet. Wie auch immer, vom Blickpunkt des Vergleichs mit analogen Filtern, führt uns das Wort Rauschen gegenüber seiner Bedeutung auf eine falsche Spur. Analoge spannungskontrollierte Filter sind häufig sehr rauschbehaftet, dies wird aber nicht als furchtbar störend angesehen. Im Gegensatz dazu werden die Artefakte der Quantisierung digitaler Tonsignale als sehr störend wahrgenommen. Daher bevorzuge ich den Ausdruck „Quantisierungsverzerrung“, welcher exakt aufzeigt, dass Quantisierung signalabhängige Tonartefakte produziert.
Quantisierungsverzerrungen entstehen, wenn die Mantisse der Signaldarstellung nicht ausreichend ist. Die allgemeine Form eines digitalen Filters führt zu einer sequentiellen Zustandsverzögerung bei der Ausgabe aus dem Filter (siehe Abbildung 1). Um den Filterzustand weiterzureichen, müssen die unterschiedlichen Verzögerungen mitgenommen werden. Diese haben ihre Ursachen in der Differenz zwischen ähnlicher, kleinerer oder gleicher Amplitude als die Mantisse dieser Werte. Wichtig an dieser Stelle ist, dass eine Fließkomma-Implementierung die Quantisierungsverzerrung, gegenüber einem „Fest-Komma-Schema“ mit derselben Mantissen Anzahl nicht verbessert. Man kann die benötigte Mantissen Anzahl unter Betrachtung eines hoch resonanten (steilflankigen) Tiefpass Filters abschätzen, wenn das Filter ohne Signal am Eingang in angeregter Resonanz schwingt. In diesem Fall ist das Ausgangssignal eine exponentiell abklingende Sinusschwingung, welche komplett aus den Filterzustandsvariablen der beiden Verzögerungen entsteht.
Betrachten wir eine Resonanz bei 20 Hz bei einer Abtastrate von 44,1 kHz. Der schlimmste anzunehmende Fall tritt am Gipfel der Amplitude einer Schwingungsform auf, wenn die Differenz zwischen 2 Abtastproben (Samples) das volle Amplitudensignal beträgt, hier ergibt sich folgende Gleichung:
(Bemerkung des Autors zum Formelverständnis:
„Dave Rossum hat hier die allgemeine Filtergleichung schon entsprechend umgestellt. Das vereinfacht zwar nicht das Verständnis, macht aber die Rechnung leichter. Die Frage ist, wie viele Nachkommastellen muss ich berechen, um mein Signal so natürlich wie möglich ausklingen zu lassen. Da wir mit 0 und 1 rechnen, benötigen wir mindestens 23 Nachkommastellen und unsere Wortbreite beträgt somit minimal 23 bit.“)
Die Differenz muss immer die gesamte Amplitude und den Frequenzgang des zeitlich verzögerten Signals abbilden. Hier, für unser Bespiel, sind mehr als 23 Bit notwendig, um den Signalverlauf, so wie er abklingt, abbilden zu können. Wir, bei E-mu, haben herausgefunden, dass sich mit 32 Bit Mantissen (Fließkomma-Zahlen) musikalische Filter mit unhörbaren Quantisierungsverzerrungen herstellen lassen.
Grenzzyklen sind das andere Problem in der Kennlinien- und Kleinsignalspezifikation von digitalen Filtern. Grenzzyklen entstehen als Ergebnis von Quantisierungsfehlern und können durch Verwendung von Fließkomma-Rechnen entsprechend klein gehalten werden. Wie auch immer, wenn ein Filter grenzzyklisches Verhalten (unter Verwendung eines endlichen Präzision A/D-Wandlers) aufzeigt, wird der Grenzzyklus zwischen dem MSB (höchstwertigem Bit) des Wandlers hin- und herschalten und produziert ein hörbares Signal oberhalb der Amplitude (Magnitude) eines nicht abgeschnittenen ausschwingenden Signals.
Grenzzyklen sind, das was ihr Name impliziert, zyklische Sequenzen, welche zur Folge haben, dass bei niedrigen Werten hörbare Signalverstimmungen entstehen. Man kann überlagerte Schwingungen (Dither) benutzen (s.a. Vanderkooy 1989), um dem Grenzzyklus weis zu machen, dass Rauschen einer ähnlichen Amplitude den Grenzzyklus aufbricht. Als Alternative kann der Grenzzyklus durch Beschränkung des Ausgangssignals (Filter) gegen Null ausgelöscht werden. Hier wird dann die große Mantisse auf wenige Bits für die weitere Verarbeitung beschränkt. Dieses Vorgehen ist besonders geeignet, wenn 32 Bit Fließkomma benutzt wird. Die Grenzzyklen sind hier klein genug, so dass Fließkomma-Rechnen nicht benötigt wird, um eine weitere Verarbeitung des Signals gut funktionieren zu lassen, insbesondere bei Werten nahe Null. Denn Abtrennung bei Werten gegen Null führen zu höheren Werten als Rundungsfehler. Diese Fehler kann man klein genug gestalten, für den Fall, dass die Differenz zweier Signale keine aussagekräftige Mantisse ergibt.
Wenn überlagerte Schwingungen oder das Abtrennen vor dem Null-Wert benutzt werden, um Grenzzyklen zu begrenzen, müssen wir Artefakte in Kauf nehmen. Überlagerte Schwingungen, wenn mit einer angebrachten Wortbreite richtig im Signalpfad eingesetzt, sind ein nützliches Werkzeug. Leider ist es normalerweise nicht der Fall, dass der Signalpfad ideal durchgestaltet wird und die Überlagerten Schwingungen erzeugen unerwünschtes Rauschen, während Abtrennung gegen Null hier theoretisch mehr Verzerrungen erzeugt. Wir haben herausgefunden, dass dies oft als erstklassige praktische Lösung wahrgenommen wird.

Von links nach rechts: Marco Alpert, Scott Wedge, Dave Rossum und Ed Rudnick anlässlich des 30. Firmenjubiläums von E-MU
- Spektrales Verhalten
Das spektrale Verhalten von digitalen Filtern kann einfach kontrolliert werden und ist einer der Hauptgründe für den Einsatz digitaler Filter. Interessanterweise haben unsere Forschungen aufgezeigt, dass spektrales Verhalten von digitalen Filtern nicht ungeheuer wichtig ist. Während der Unterschied zwischen einem Filter 2. und 4. Ordnung klar hörbar ist, ist die relative Platzierung der Filterpole nicht sonderlich kritisch.
Frühere analoge Filter benutzen Allpassfilter, typischerweise 2 Pol oder 4 Pol Tiefpass. Digitale Filter benutzen oftmals ähnliche Implementierungen des Allpassfilters oder Auto Regressive Modelle für dynamische Filter. Digitale Filter arbeiten mit einer festen Abtastrate. Als Ergebnis daraus erreichen wir keine asymptotische Flankensteilheit von 6 dB/Oktave pro Filterpol, am oberen Ende des hörbaren Frequenzbereiches. Anstelle dessen und unter Berücksichtigung der Verwandtschaft der Flankensteilheit mit einer Cosinus-Funktion, pegelt sich die Flankensteilheit bei hohen Frequenzen ein. Dies kann glücklicherweise durch einen „Nullwert-Verfolger“ sehr gut kompensiert werden.
- Dynamisches Verhalten
Dass analoge Filter spannungskontrolliert werden können, ist die interessanteste Fähigkeit von klassischen analogen Filtern. Mit anderen Worten, der Filter Cutoff wobbelt durch die Entwicklung einer Musiknote. Es war dieses Verhalten, das den „Synthesizer“ Sound für das Publikum interessant machte. Als Ergebnis daraus erhielten digitale Filter einen analogen Klang, in dem ihre Dynamik richtig angesteuert wurde.
Die Filtersteuerung mit der richtigen Hüllkurve ist wichtig. Alle digitalen Filter Koeffizienten haben ihren direkten Bezug zur Filter Cutoff Frequenz. Die natürliche Kontrolle und Steuerung ist anders als zur exponentiellen (Volt pro Oktave) Steuerung analoger Filter. Konsequenterweise muss hier eine Parameterumformung stattfinden, so lineares Ansteigen einer Steuer Variablen (z. B. durch einen MIDI-Controller) ein exponentielles Ansteigen der Filter Cutoff Frequenz erzeugt. Dies kann durch eine Mapping (Vermessungs-) Funktion oder direktes Umrechnen der Filterkoeffizienten erfolgen (Rossum 1991).
Die Filter Koeffizienten eines Filters werden als solches auch gefiltert. Bedenken wir ein typisches Rückkopplungsfilter, siehe auch Abbildung 1. Wenn sich die Koeffizienten ändern, hat das unmittelbar Auswirkungen auf die Amplitude des rückgekoppelten Signals, welche einen zeitlichen Abbruch in eben diesem Signal verursacht. Dies ist gleichbedeutend mit einem zeitlichen Abbruch am Signaleingang, da sich Rückkopplungssignal und Eingangssignal summieren. Das Filter-Ausgangssignal wird konsequenterweise auf demselben Weg beeinflusst wie bei einer Signaländerung. Somit werden die Effekte einer Koeffizientenänderung nicht stetig, also unstetig, gefiltert, sie sind gleich mit der Rückkopplungsfrequenz des Eingangssignals.
Um die Bandbreite der Koeffizienten Änderung zu begrenzen, müssen die Koeffizienten mit der Abtastrate geändert werden. Änderungen bei niedrigen Spannungswerten führen zu hörbaren Signalabbildungen mit dem Wert der Änderungsrate im Signalweg, welche nur ein wenig durch Filtern beeinflusst werden können.
- Großsignalverhalten
Der größte Beitrag zu dem „analogen“ Klang von Filtern ist das Großsignal „Verzerrungs“-Verhalten. In den 1970er Jahren wurde der charakteristische Moog Sound von vielen Musikern geschätzt. Moog hatte eine patentierte spannungskontrollierte Filterstruktur (Moog 1969), welche eine einzigartige Verzerrungscharakteristik hatte, total verschieden zu anderen Schaltungstechniken, wie die spannungskontrollierten Filter Implementationen von Verstärkern mit feststehender Übertragungskennlinie
(Anmerkung: „hier bezogen auf die Flankensteilheit.“)
Die Kennlinie dieser Verzerrung war die primäre Quelle des „Moog“ Klanges.
(Anmerkung: „gemeint ist die Einstellbarkeit der Kennlinie“)
Analoge spannungskontrollierte Filter, hier der „Moog Ladder“ Filter oder Verstärker mit feststehender Übertragungskennlinie sind abhängig vom „S“-förmigen Antwortverhalten des Transistorpaares eines Differenzverstärkers. Die Charakteristik dieser Schaltung führt zu einem sanften Abschneiden. Weiterhin wirkt dieses Abschneiden auch auf den Eingang des Filters, so dass unser Ergebnis ebenso gefiltert wird.
In digitalen Filtern benötigen wir eine Form des Schutzes von Überlastungen, da die Schaltung steuerbar ist. Bestimmte Eingangssignale werden genügend Energie in der Nähe der Filter Resonanz haben, welche ein Ausgangssignal größer als der numerische Spannungswert des Algorithmus haben (oder des D/A-Wandlers). Sättigungsalgorithmen werden üblicherweise genutzt, um dieses Problem zu lösen. Im Allgemeinem finden man diese im Speicher des Filters. Hierdurch erhalten wir eine extrem scharfe Kennliniengrenze, das Filter arbeitet perfekt linear bis zur Sättigung und darüber wird das Signal stark verzerrt. Das gibt den üblichen digitalen Filtern ein raues Klangverhalten, wenn sie übersteuert werden.
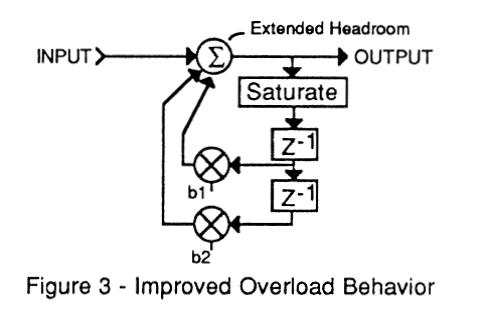
Glücklicherweise können wir das mit einer Annäherung an ein Filter 1. Ordnung (Tiefpass) beheben, wir geben dem Filter einen Spielraum, wenn wir dem Speicheranteil des Filter einen Spielraum geben und wenn wir nur sättigen, falls die Signalverzögerungen vor den verschiedenen Eingangssignalen anliegen. Wie in Abbildung 3 sichtbar ist, erzeugen wir die Sättigung am Eingang des Filters. Dies ist analog genug zum analogen Differenzverstärker.
Dabei wird die Kennlinie zu einer „S“-Kurve. Das digitale Filter hat eine „schärfere“ Z-Kennlinie, die Ähnlichkeit ist hörbar.
Nichtlineare Systeme haben sehr viel Aufmerksamkeit erhalten, wir finden in ihnen komplexe Vorgänge, die komplexen Naturphänomenen sehr ähnlich sind. Interessanterweise ist das zuvor erläuterte Schema digitaler Filter-(Verzerrungen), ein Resultat aus dem Phänomen nicht idealer analoger Filter. Man wird sich hier beim Experimentieren mit den Filtern die Tage der analogen Synthese deutlich erinnern, als ein angeregtes Filter bis zu einer Großsignal Resonanz getrieben wurde, ein Eingangssignal zieht die Resonanz weg von seiner Nennfrequenz. Im übertragenen Sinne, wenn das Eingangssignal die Resonanz entfernt, der Filter klingelt (wobbelt) runter mit einer deutlich hörbaren Frequenzänderung beim Resonanzanschlag. Das macht die Natur der „analogen“ Filter hörbar und sehr überzeugend.
Die Ursache dieses Verhaltens kann unter Betrachtung der Sättigung der Eingänge zu den Verstärkern verstanden werden. Wenn dies Auftritt kann jemand sagen, das Signal ist gesättigt (obwohl dies ein kleineres Ergebnis am Ausgang des Verstärkers produziert) oder alternativ das der Koeffizient derartig reduziert wurde, dass er das selbe kleine Ergebnis ausgibt. Betrachtet man dies als Ausweg, ist es offensichtlich, dass der Anfang der Verzerrung gleichbedeutend ist mit einer Koeffizientenänderung der Filter.
Wie zuvor ausgeführt, die Koeffizienten werden als solches ebenso gefiltert.
Der Punkt, dass die Koeffizienten sich ändern abhängig von der derzeitigen Sättigung des Signals, führt nicht zu einer grässlichen Verzerrung. In diesem Sinne kann man sagen, dass die Konsequenz des Schemas des Überlastungsschutzes ändert die Koeffizienten, dass die Signaleingabe nicht länger das Filter überlastet (verzerrt).
Es ist klar, dass zusätzliche Techniken angewendet werden müssen, um eine charakteristische Filterverzerrung zu treffen und die Kennlinien charakteristischer analoger „Vintage“ Synthesizer nachzubilden, den ganzen langen Weg zu einem digitalem „SPICE“ Modell eines Filters.
Aber die zuvor angeführten Techniken zeigen, dass sorgfältiger Entwurf, kleine Änderungen an der Normalform von digitalen Filtern notwendig ist, um ein analoges Verhalten zu erzeugen, inklusive einiger sehr interessanter nicht linearer Effekte.
Wir glauben, dass der Beweis für unser Erfolg durch den „EMAX II“ Test von „Sound on Sound“ (Wrigthson, 1989) geführt wurde, welcher die „Wärme“ der „analog“ klingenden E-mu Filter beschrieb und anpries. 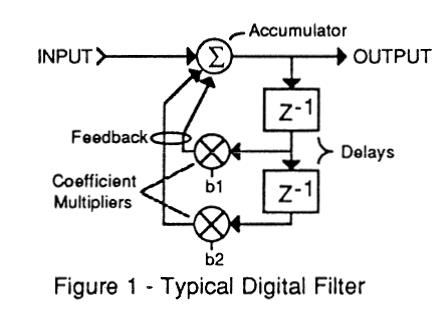
Abbilung 1 : Typisches digitaler Filter
Abbildung 3 : Verbesserter Filter mit überlastbarem Filterverhalten
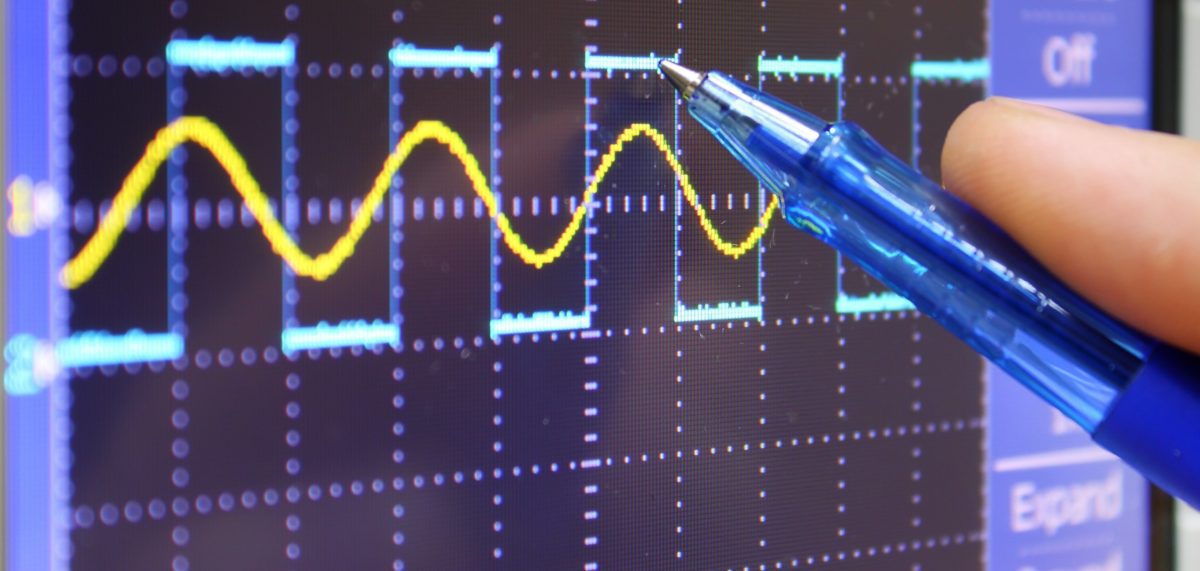
Abbildung 2: Tiefpass Filter Antworten





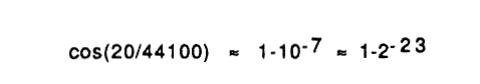










Nett. Ich würde den Artikel doch lieber ganz im Original lesen. Bitte fügt noch den link hinzu.